Let’s find ways to test congruence of interesting figures.
Trapezoids $ABCD$ and $A’B’C’D’$ are congruent.
Are any of the ovals congruent to one another? Explain how you know.
You can use 12 toothpicks to create a polygon with an area of five square toothpicks, like this:
Can you use exactly 12 toothpicks to create a polygon with an area of four square toothpicks?
Here are two congruent shapes with some corresponding points labeled.
Draw the points corresponding to $B$, $D$, and $E$, and label them $B’$, $D’$, and $E’$.
Draw line segments $AD$ and $A’D’$ and measure them. Do the same for segments $BC$ and $B’C’$ and for segments $AE$ and $A’E’$. What do you notice?
Do you think there could be a pair of corresponding segments with different lengths? Explain.
Are these faces congruent? Explain your reasoning.
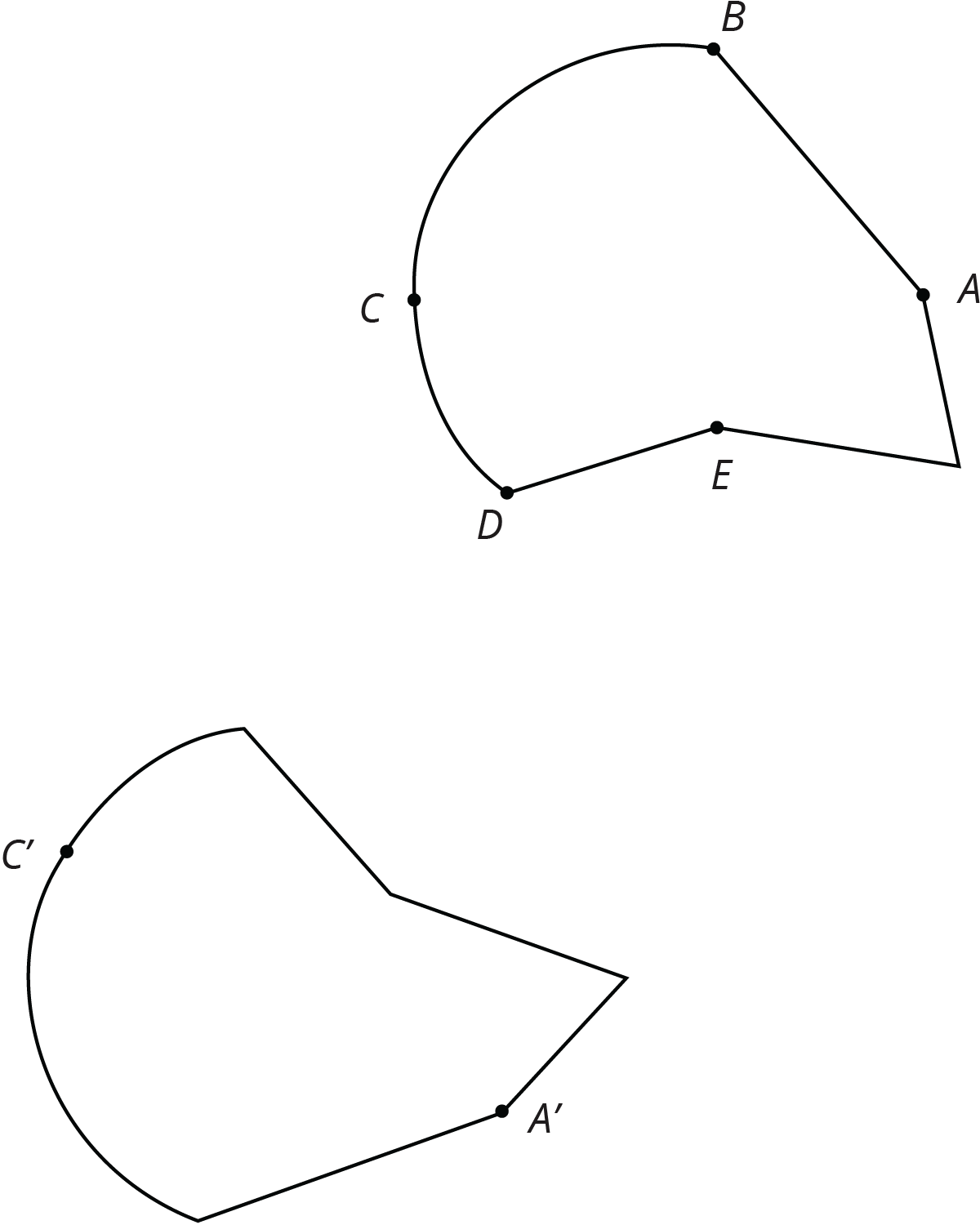
To show two figures are congruent, you align one with the other by a sequence of rigid transformations. This is true even for figures with curved sides. Distances between corresponding points on congruent figures are always equal, even for curved shapes. For example, corresponding segments $AB$ and $A'B'$ on these congruent ovals have the same length:
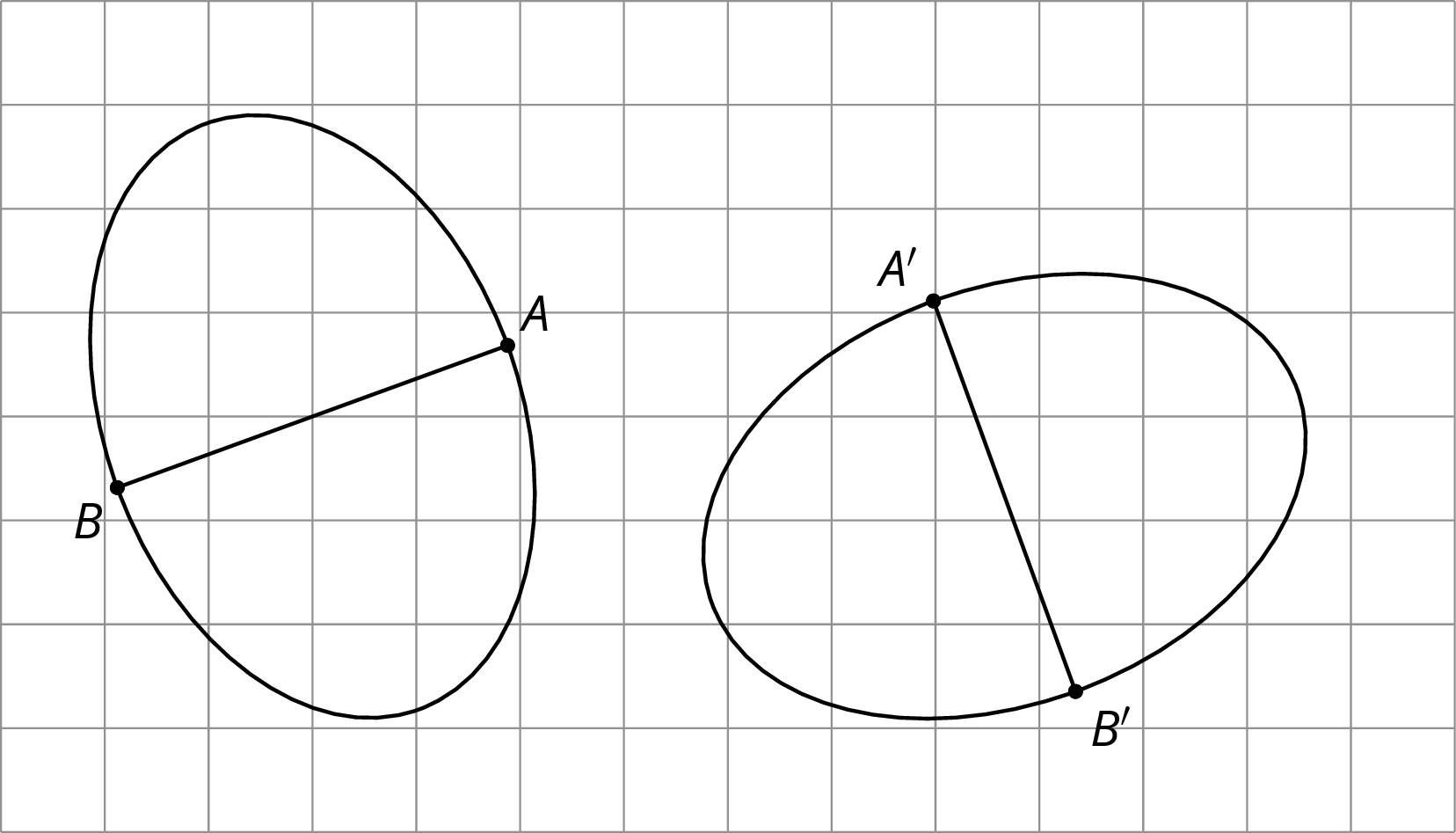
To show two figures are not congruent, you can find parts of the figures that should correspond but that have different measurements.
For example, these two ovals don’t look congruent.
On both, the longest distance is 5 units across, and the longest distance from top to bottom is 4 units. The line segment from the highest to lowest point is in the middle of the left oval, but in the right oval, it’s 2 units from the right end and 3 units from the left end. This proves they are not congruent.
