16.1: True or False: Computational Relationships
Is each equation true or false?
$62-28= 60-30$
$3\boldcdot \text{-}8= (2\boldcdot \text{-}8) - 8$
Let’s see why the angles in a triangle add to 180 degrees.
Is each equation true or false?
$62-28= 60-30$
$3\boldcdot \text{-}8= (2\boldcdot \text{-}8) - 8$
Here is triangle $ABC$.
Select the Midpoint tool  and click on two points or a segment to find the midpoint.
and click on two points or a segment to find the midpoint.
Rotate triangle $ABC$ $180^\circ$ around the midpoint of side $AC$. Right click on the point and select Rename to label the new vertex $D$.
Rotate triangle $ABC$ $180^\circ$ around the midpoint of side $AB$. Right click on the point and select Rename to label the new vertex $E$.
Look at angles $EAB$, $BAC$, and $CAD$. Without measuring, write what you think is the sum of the measures of these angles. Explain or show your reasoning.
Is the measure of angle $EAB$ equal to the measure of any angle in triangle $ABC$? If so, which one? If not, how do you know?
Is the measure of angle $CAD$ equal to the measure of any angle in triangle $ABC$? If so, which one? If not, how do you know?
What is the sum of the measures of angles $ABC$, $BAC$, and $ACB$?
Here is $\triangle ABC$. Line $DE$ is parallel to line $AC$.
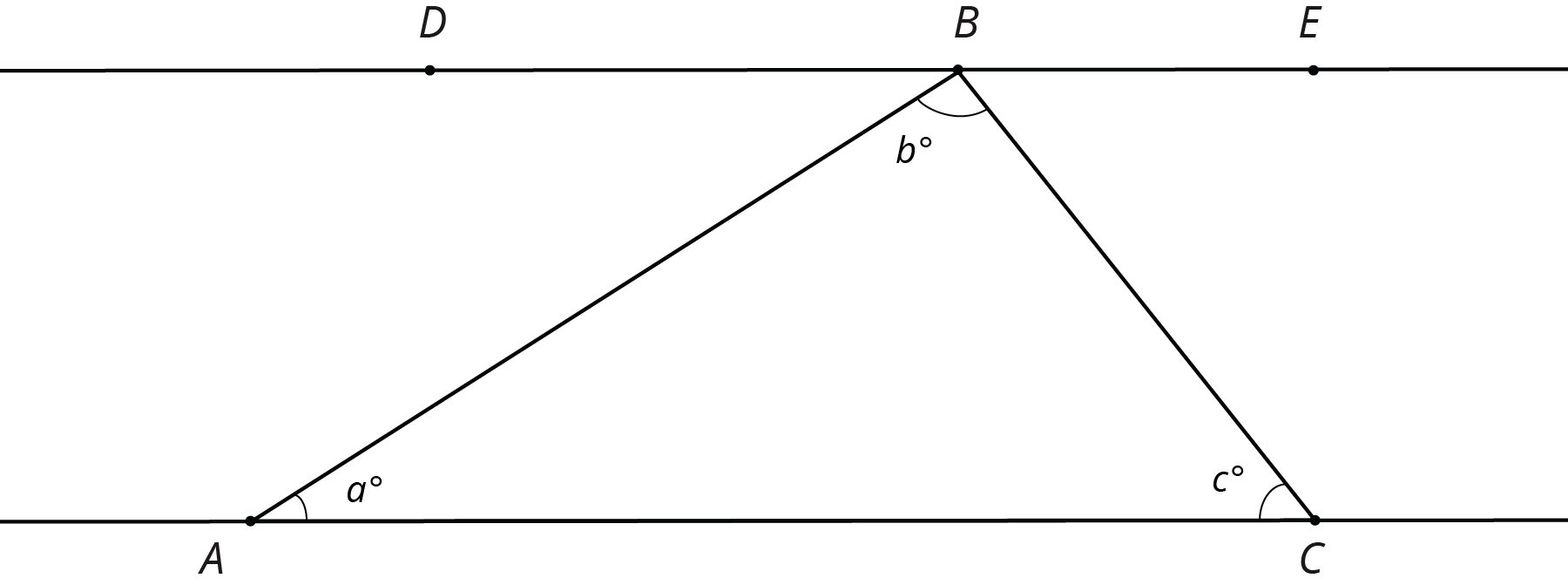
What is $m{\angle DBA} + b + m{\angle CBE}$? Explain how you know.
Explain why your argument will work for any triangle: that is, explain why the sum of the angle measures in any triangle is $180^\circ$.
Using a ruler, create a few quadrilaterals. Use a protractor to measure the four angles inside the quadrilateral. What is the sum of these four angle measures?
This diagram shows a square $BDFH$ that has been made by images of triangle $ABC$ under rigid transformations.

Using parallel lines and rotations, we can understand why the angles in a triangle always add to $180^\circ$. Here is triangle $ABC$. Line $DE$ is parallel to $AC$ and contains $B$.
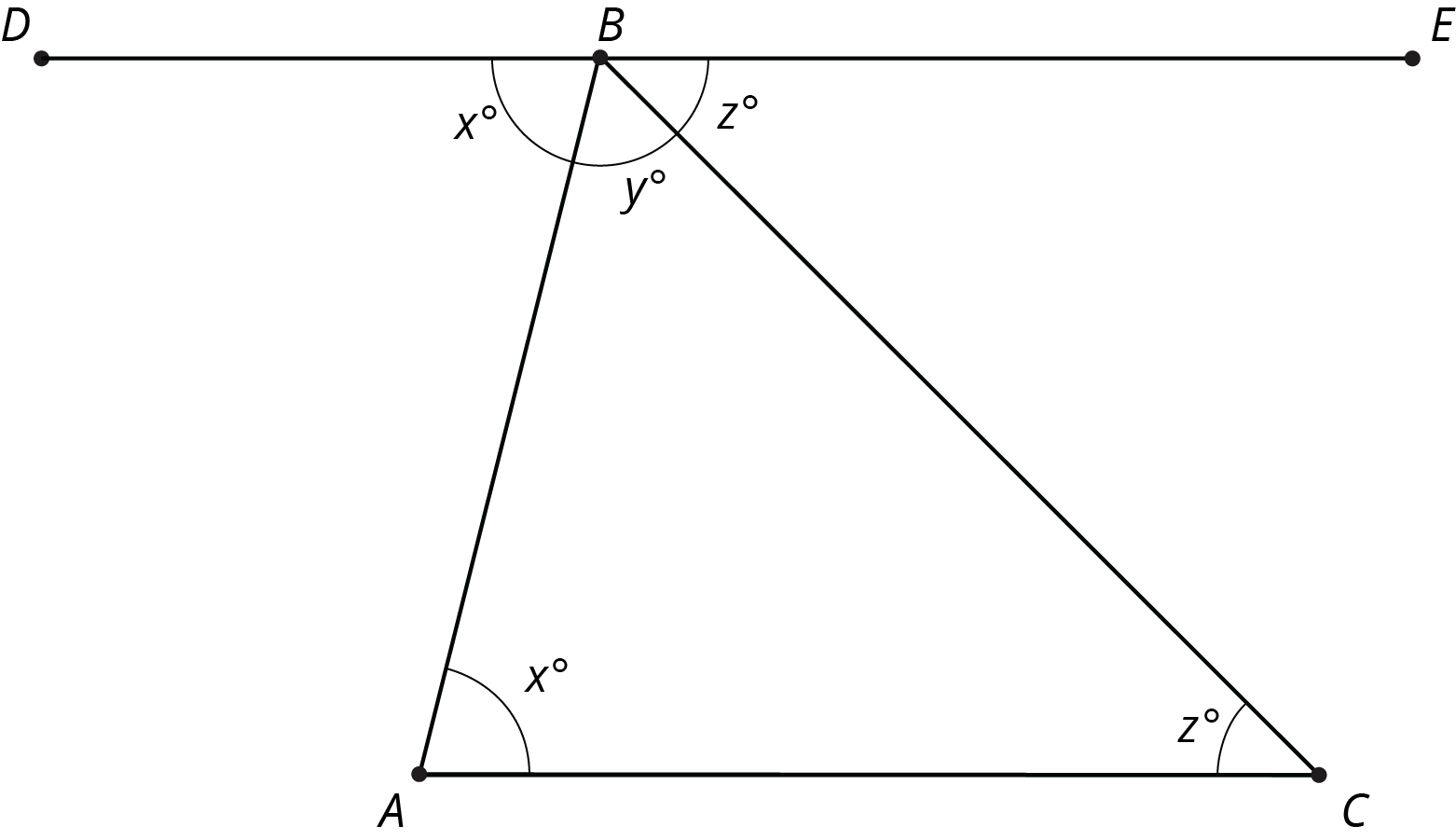
A 180 degree rotation of triangle $ABC$ around the midpoint of $AB$ interchanges angles $A$ and $DBA$ so they have the same measure: in the picture these angles are marked as $x^\circ$. A 180 degree rotation of triangle $ABC$ around the midpoint of $BC$ interchanges angles $C$ and $CBE$ so they have the same measure: in the picture, these angles are marked as $z^\circ$. Also, $DBE$ is a straight line because 180 degree rotations take lines to parallel lines. So the three angles with vertex $B$ make a line and they add up to $180^\circ$ ($x + y + z = 180$). But $x, y, z$ are the measures of the three angles in $\triangle ABC$ so the sum of the angles in a triangle is always $180^\circ$!