6.1: Finding a Center of Rotation
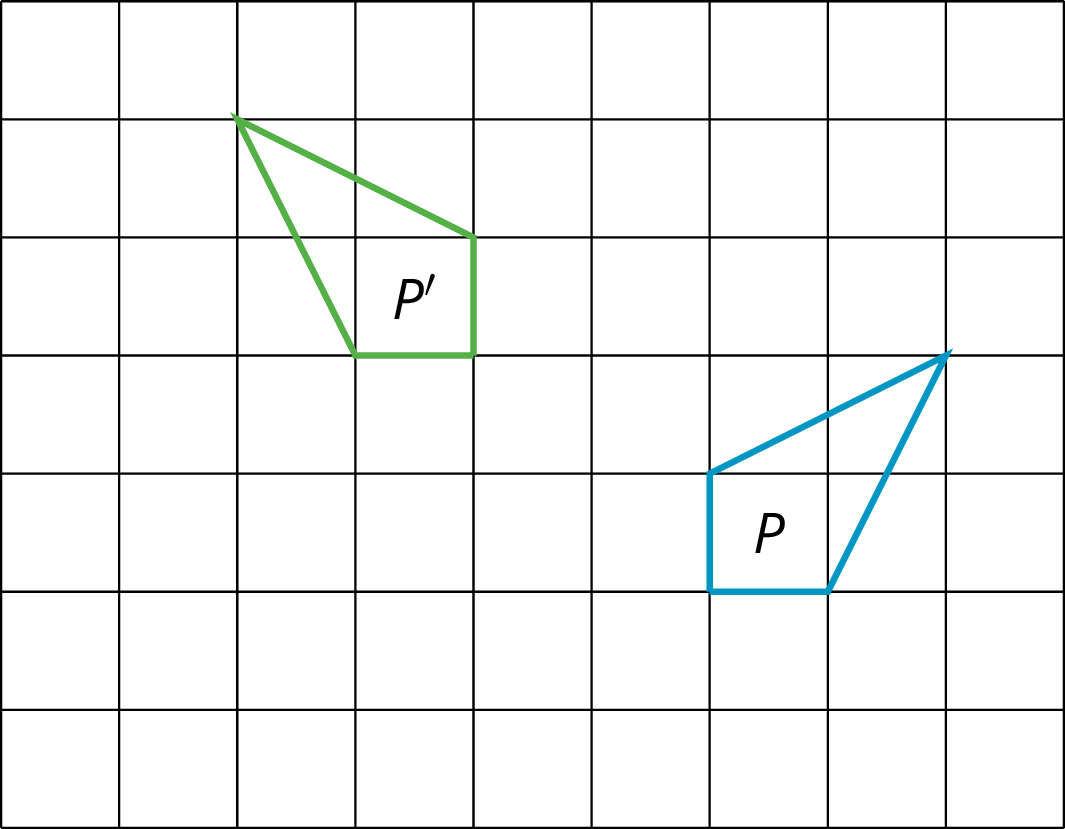
Andre performs a 90-degree counterclockwise rotation of Polygon P and gets Polygon P’, but he does not say what the center of the rotation is. Can you find the center?
Let’s transform some polygons in the coordinate plane.
Andre performs a 90-degree counterclockwise rotation of Polygon P and gets Polygon P’, but he does not say what the center of the rotation is. Can you find the center?

Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
If your teacher gives you the data card:
Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.
Sometimes two transformations, one performed after the other, have a nice description as a single transformation. For example, instead of translating 2 units up followed by translating 3 units up, we could simply translate 5 units up. Instead of rotating 20 degrees counterclockwise around the origin followed by rotating 80 degrees clockwise around the origin, we could simply rotate 60 degrees clockwise around the origin.
Can you find a simple description of reflecting across the $x$-axis followed by reflecting across the $y$-axis?
The center of a rotation for a figure doesn’t have to be one of the points on the figure. To find a center of rotation, look for a point that is the same distance from two corresponding points. You will probably have to do this for a couple of different pairs of corresponding points to nail it down.
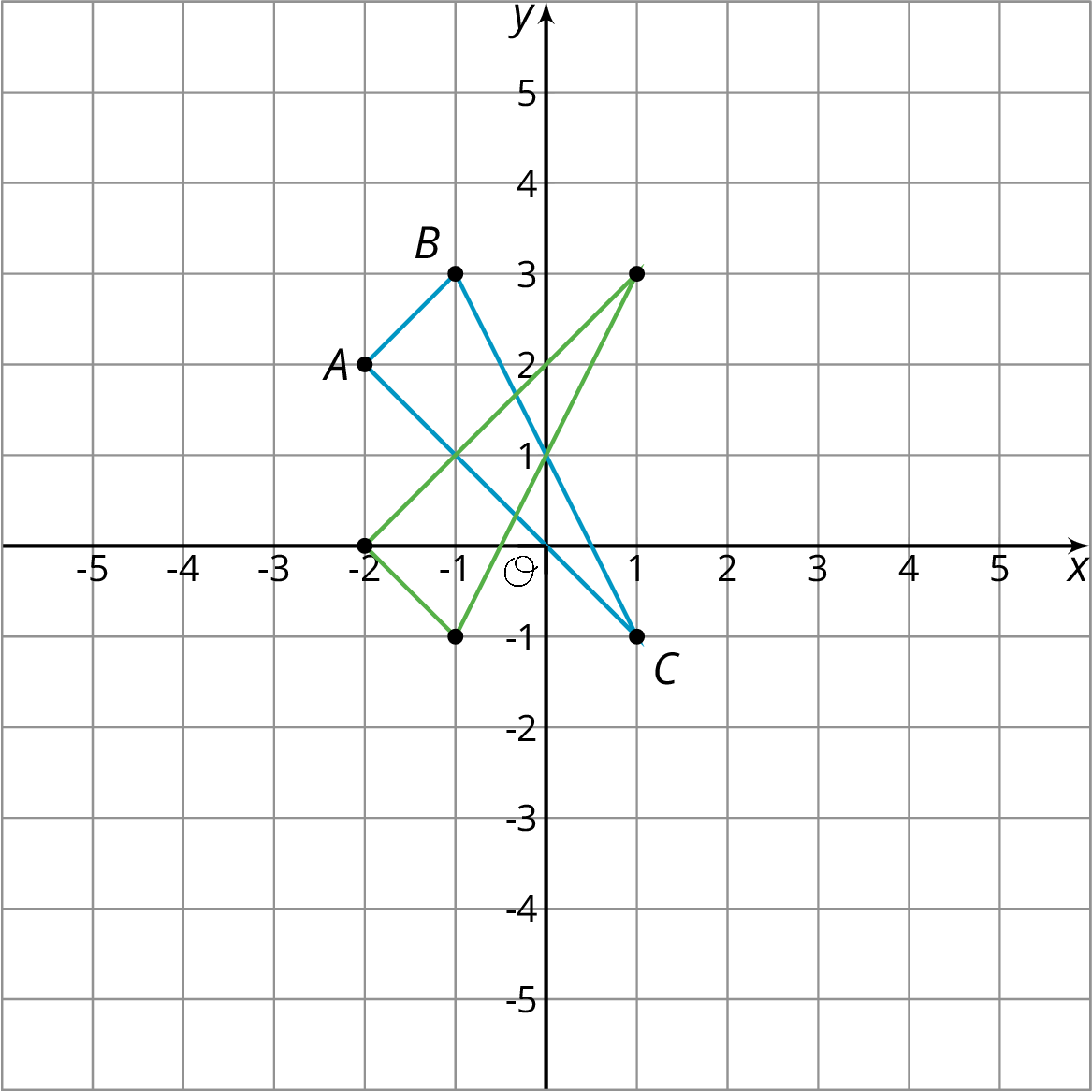
When we perform a sequence of transformations, the order of the transformations can be important. Here is triangle $ABC$ translated up two units and then reflected over the $x$-axis.
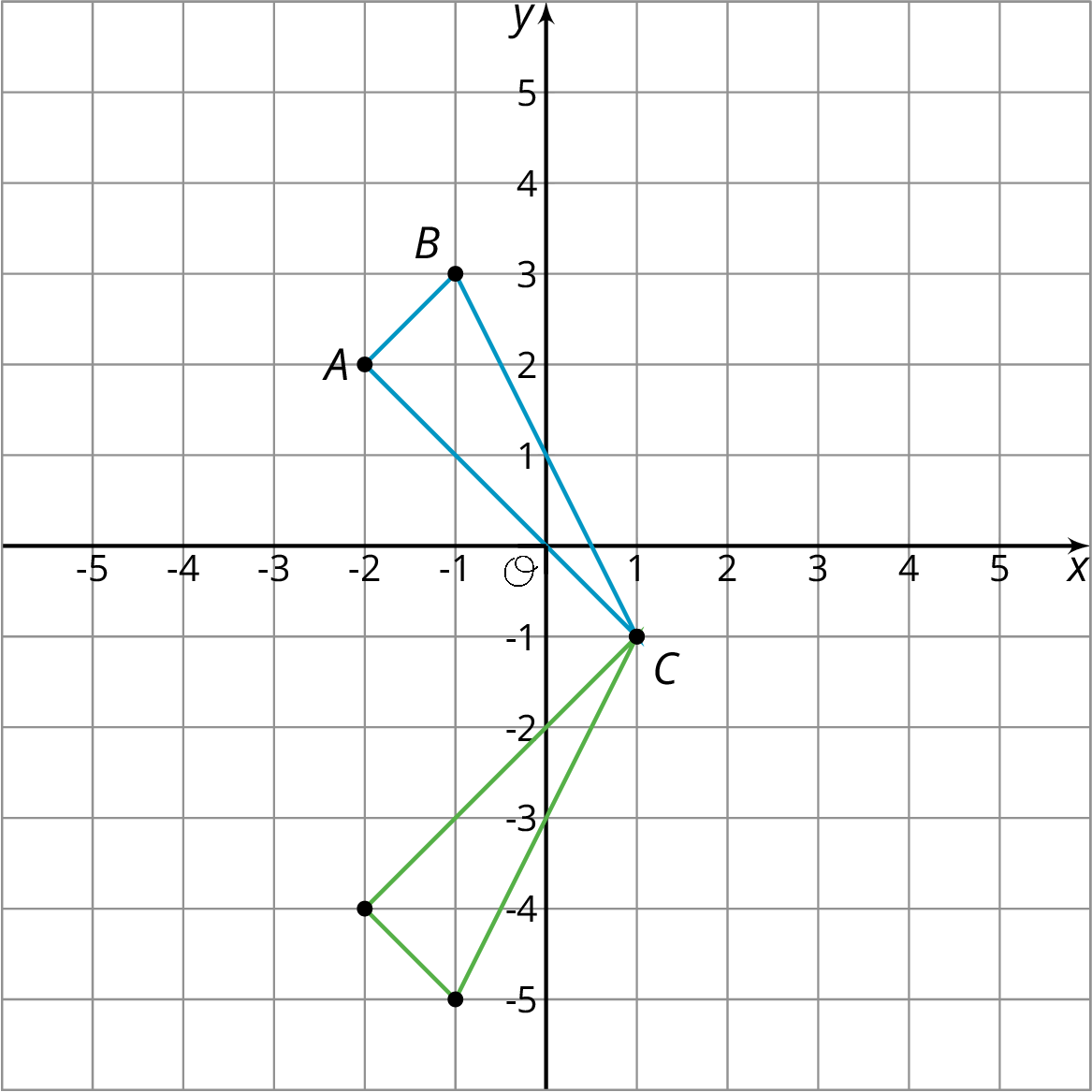
Here is triangle $ABC$ reflected over the $x$-axis and then translated up two units.
Triangle $ABC$ ends up in different places when the transformations are applied in the opposite order!