10.1: Equal Quotients
Write some numbers that are equal to $15 \div 12$.
Let’s learn about the slope of a line.
Write some numbers that are equal to $15 \div 12$.
The figure shows three right triangles, each with its longest side on the same line.
Your teacher will assign you two triangles. Explain why the two triangles are similar.

| triangle | vertical side | horizontal side | (vertical side) $\div$ (horizontal side) | |
|---|---|---|---|---|
| row 1 | $ABC$ | |||
| row 2 | $CDE$ | |||
| row 3 | $FGH$ |
Here are several lines.

Here is a line drawn on a grid. There are also four right triangles drawn. Do you notice anything the triangles have in common?

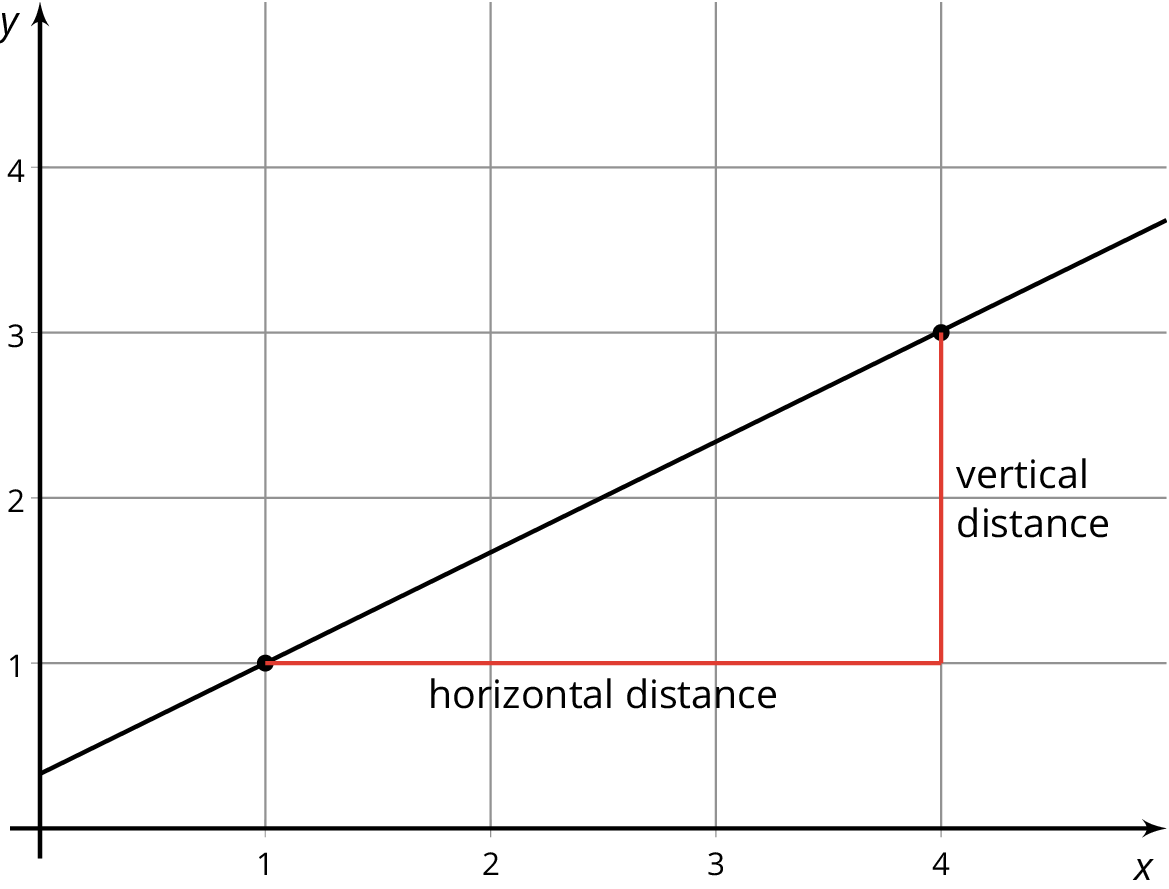
These four triangles are all examples of slope triangles. One side of a slope triangle is on the line, one side is vertical, and another side is horizontal. The slope of the line is the quotient of the length of the vertical side and the length of the horizontal side of the slope triangle. This number is the same for all slope triangles for the same line because all slope triangles for the same line are similar.
In this example, the slope of the line is $\frac{2}{3}$, which is what all four triangles have in common. Here is how the slope is calculated using the slope triangles:
The slope of a line is the quotient of the vertical distance and the horizontal distance between any two points on the line.