3.1: Points on a Ray
- Find and label a point $C$ on the ray whose distance from $A$ is twice the distance from $B$ to $A$.
- Find and label a point $D$ on the ray whose distance from $A$ is half the distance from $B$ to $A$.

Let’s dilate figures not on grids.

Dilate $B$ using a scale factor of 5 and $A$ as the center of dilation. Which point is its image?
Using $H$ as the center of dilation, dilate $G$ so that its image is $E$. What scale factor did you use?
Using $H$ as the center of dilation, dilate $E$ so that its image is $G$. What scale factor did you use?
To dilate $F$ so that its image is $B$, what point on the diagram can you use as a center?
Dilate $H$ using $A$ as the center and a scale factor of $\frac{1}{3}$. Which point is its image?
Describe a dilation that uses a labeled point as its center and that would take $F$ to $H$.
Using $B$ as the center of dilation, dilate $H$ so that its image is itself. What scale factor did you use?
Follow the directions to perform the dilations in the applet.

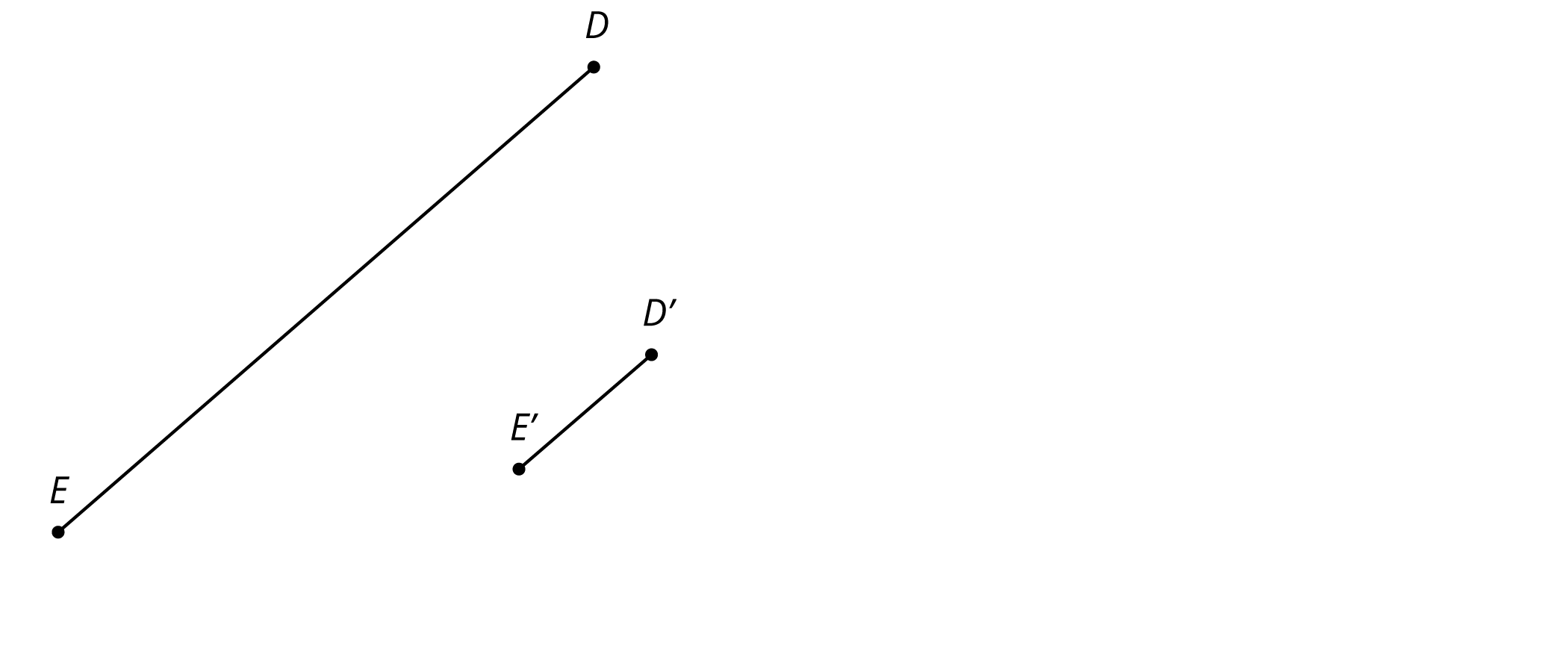
Here is line segment $DE$ and its image $D’E’$ under a dilation.
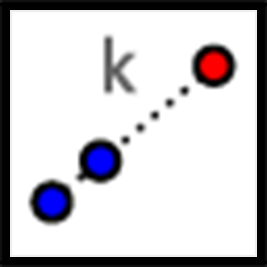
If $A$ is the center of dilation, how can we find which point is the dilation of $B$ with scale factor 2?
 Since the scale factor is larger than 1, the point must be farther away from $A$ than $B$ is, which makes $C$ the point we are looking for. If we measure the distance between $A$ and $C$, we would find that it is exactly twice the distance between $A$ and $B$.
Since the scale factor is larger than 1, the point must be farther away from $A$ than $B$ is, which makes $C$ the point we are looking for. If we measure the distance between $A$ and $C$, we would find that it is exactly twice the distance between $A$ and $B$.
A dilation with scale factor less than 1 brings points closer. The point $D$ is the dilation of $B$ with center $A$ and scale factor $\frac{1}{3}$.