Let’s explore similar figures.
Use what you know about operations and their properties to write three expressions equivalent to the expression shown.
$$10 (2 + 3) - 8 \boldcdot 3$$
Triangle $EGH$ and triangle $LME$ are similar. Find a sequence of translations, rotations, reflections, and dilations that shows this.
Hexagon $ABCDEF$ and hexagon $HGLKJI$ are similar. Find a sequence of translations, rotations, reflections, and dilations that shows this.
The same sequence of transformations takes Triangle A to Triangle B, takes Triangle B to Triangle C, and so on. Describe a sequence of transformations with this property.
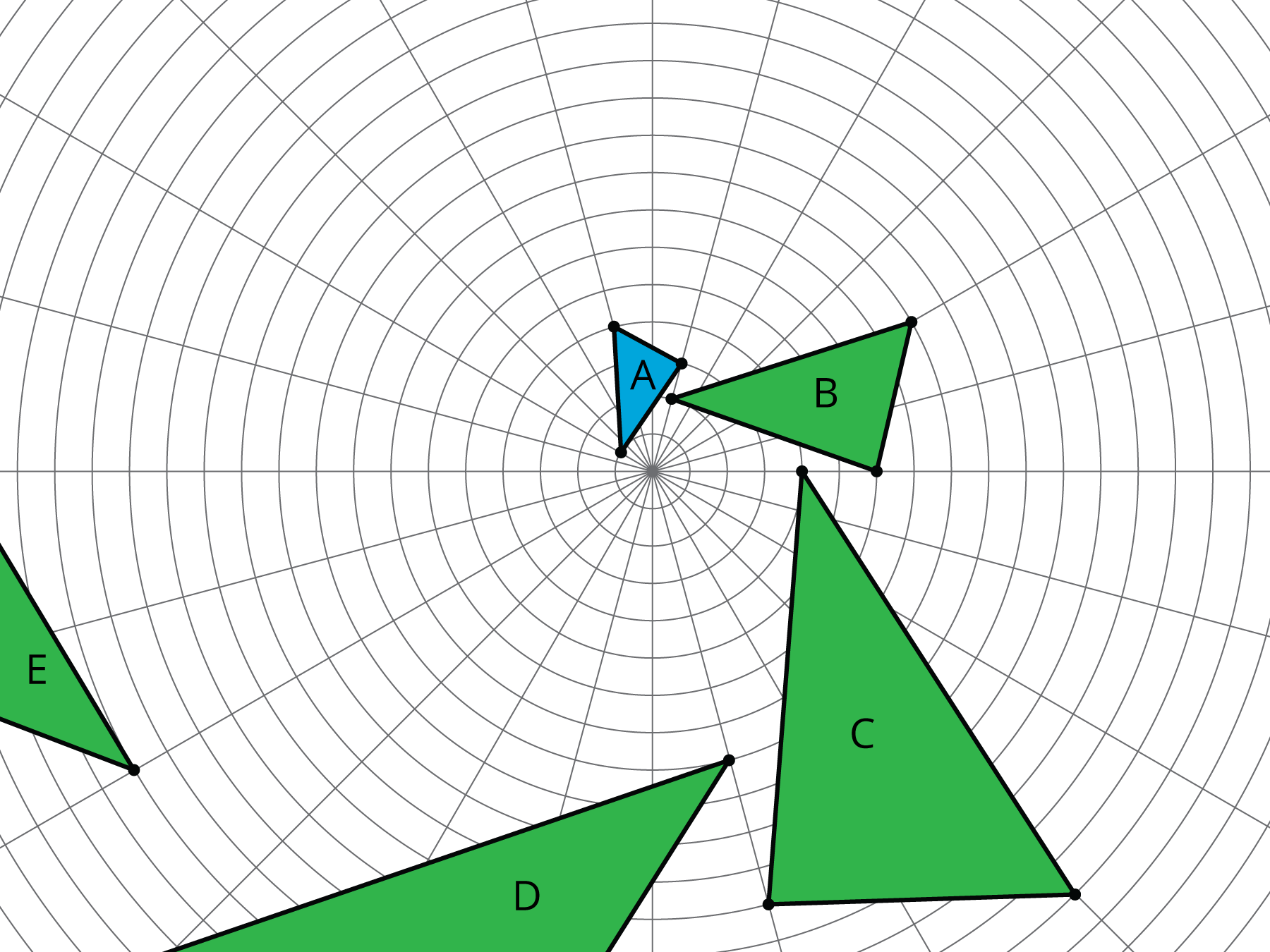
Sketch figures similar to Figure A that use only the transformations listed to show similarity.
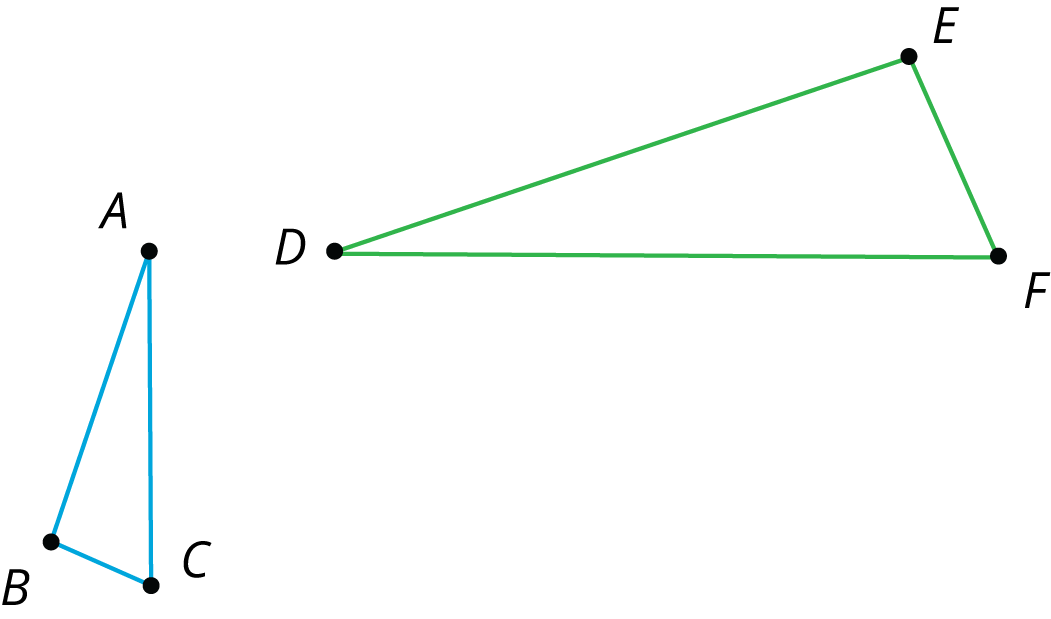
Your teacher will give you a set of five cards and your partner a different set of five cards. Using only the cards you were given, find at least one way to show that triangle $ABC$ and triangle $DEF$ are similar. Compare your method with your partner’s method. What is the same about your methods? What is different?
Let’s show that triangle $ABC$ is similar to triangle $DEF$:
Two figures are similar if one figure can be transformed into the other by a sequence of translations, rotations, reflections, and dilations. There are many correct sequences of transformations, but we only need to describe one to show that two figures are similar.
One way to get from $ABC$ to $DEF$ follows these steps:
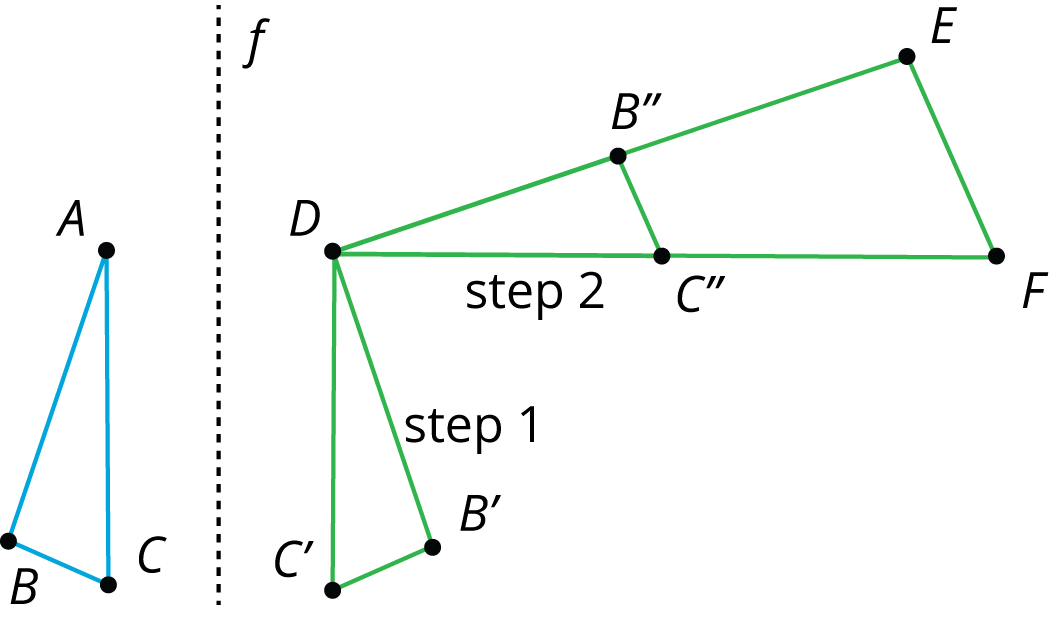
Another way would be to dilate triangle $ABC$ by a scale factor of 2 with center of dilation $A$, then translate $A$ to $D$, then reflect over a vertical line through $D$, and finally rotate it so it matches up with triangle $DEF$. What steps would you choose to show the two triangles are similar?
One figure is similar to another if there is a sequence of rigid transformations and dilations that moves the first figure so that it fits exactly over the second.
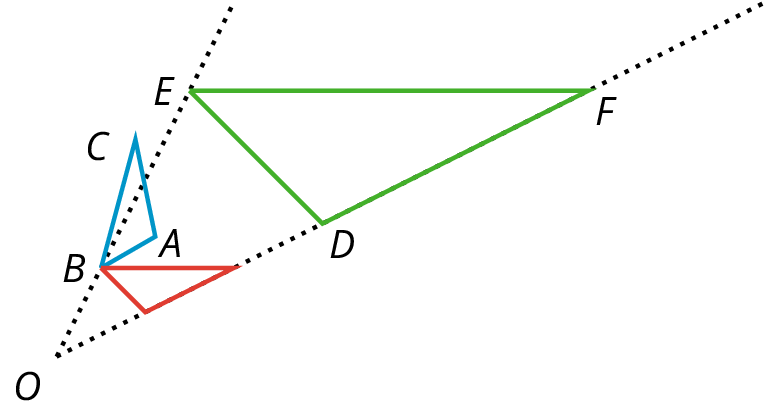
Triangle $ABC$ is similar to triangle $DEF$ because a rotation about $B$ followed by a dilation with center $O$ takes the first triangle to the second.
