9.1: Two-three-four and Four-five-six
Triangle $A$ has side lengths 2, 3, and 4. Triangle $B$ has side lengths 4, 5, and 6. Is Triangle $A$ similar to Triangle $B$?
Let’s find missing side lengths in triangles.
Triangle $A$ has side lengths 2, 3, and 4. Triangle $B$ has side lengths 4, 5, and 6. Is Triangle $A$ similar to Triangle $B$?
Your teacher will assign you one of the three columns in the second table.
Triangle $ABC$ is similar to triangles $DEF$, $GHI$, and $JKL$. The scale factors for the dilations that show triangle $ABC$ is similar to each triangle are in the table.
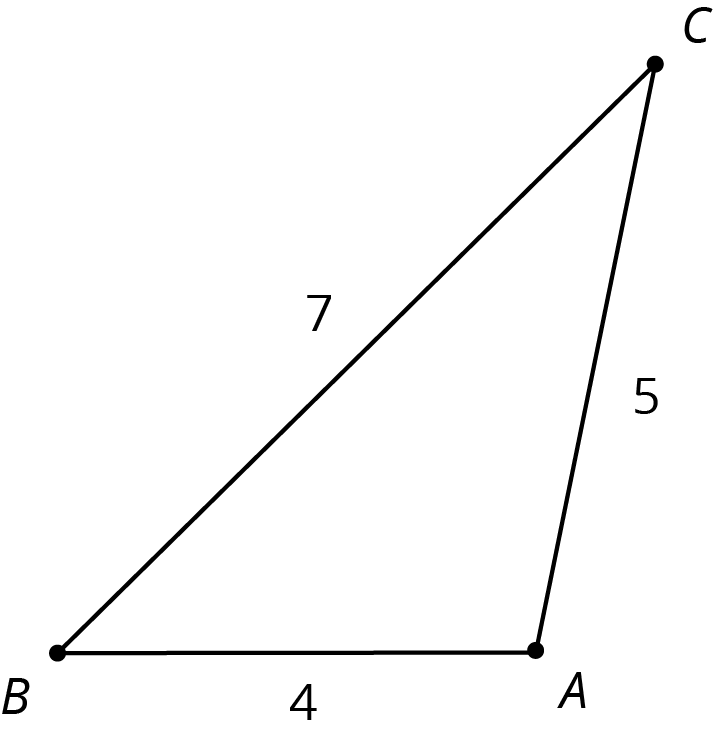
| triangle | scale factor | length of short side | length of medium side | length of long side | |
|---|---|---|---|---|---|
| row 1 | $ABC$ | 1 | 4 | 5 | 7 |
| row 2 | $DEF$ | 2 | |||
| row 3 | $GHI$ | 3 | |||
| row 4 | $JKL$ | $\frac{1}{2}$ |
| triangle | (long side) $\div$ (short side) | (long side) $\div$ (medium side) | (medium side) $\div$ (short side) | |
|---|---|---|---|---|
| row 1 | $ABC$ | $\frac{7}{4}$ or $1.75$ | ||
| row 2 | $DEF$ | |||
| row 3 | $GHI$ | |||
| row 4 | $JKL$ |
For all four triangles, find the quotient of the triangle side lengths assigned to you and record them in the second table. What do you notice about the quotients?
Triangles $ABC$ and $DEF$ are similar. Explain why $\frac{AB}{BC} = \frac{DE}{EF}$.
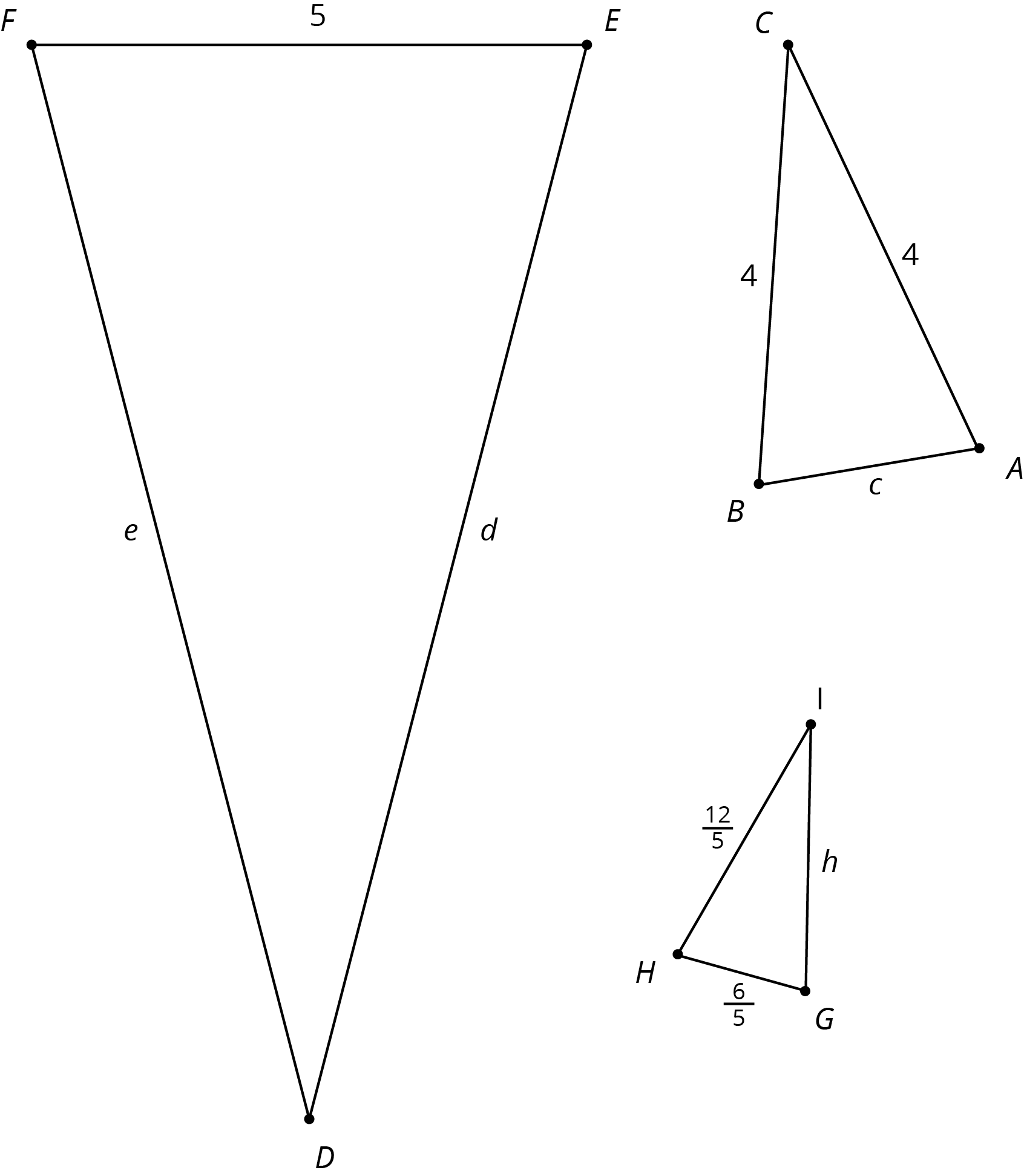
Triangles $ABC$, $EFD$, and $GHI$ are all similar. The side lengths of the triangles all have the same units. Find the unknown side lengths.
If two polygons are similar, then the side lengths in one polygon are multiplied by the same scale factor to give the corresponding side lengths in the other polygon. For these triangles the scale factor is 2:

Here is a table that shows relationships between the short and medium length sides of the small and large triangle.
| small triangle | large triangle | ||
|---|---|---|---|
| row 1 | medium side | 4 | 8 |
| row 2 | short side | 3 | 6 |
| row 3 | (medium side) $\div$ (short side) | $\frac{4}{3}$ | $\frac{8}{6} = \frac{4}{3}$ |
The lengths of the medium side and the short side are in a ratio of $4:3$. This means that the medium side in each triangle is $\frac43$ as long as the short side.
We can use these facts to calculate missing lengths in similar polygons. For example, triangles $A’B’C’$ and $ABC$ shown here are similar. Let's find the length of segment $B’C’$.

In triangle $ABC$, side $BC$ is twice as long as side $AB$, so this must be true for any triangle that is similar to triangle $ABC$. Since $A'B'$ is 1.2 units long and $2\boldcdot 1.2 = 2.4$, the length of side $B’C’$ is 2.4 units.