3.1: Number Talk: Multiplication
Find the value of each product mentally.
$15 \boldcdot 2$
$15 \boldcdot 0.5$
$15 \boldcdot 0.25$
$15 \boldcdot (2.25)$
Let's graph proportional relationships.
Find the value of each product mentally.
$15 \boldcdot 2$
$15 \boldcdot 0.5$
$15 \boldcdot 0.25$
$15 \boldcdot (2.25)$
Here are two ways to represent a situation.
Description: Jada and Noah counted the number of steps they took to walk a set distance. To walk the same distance,
Then they found that when Noah took 15 steps, Jada took 12 steps.
Equation: Let $x$ represent the number of steps Jada takes and let $y$ represent the number of steps Noah takes. $$y=\frac54x$$
Create a table that represents this situation with at least 3 pairs of values.
Graph this relationship and label the axes.

How can you see or calculate the constant of proportionality in each representation? What does it mean?
Explain how you can tell that the equation, description, graph, and table all represent the same situation.
Here are two ways to represent a situation.
Description: The Origami Club is doing a car wash fundraiser to raise money for a trip. They charge the same price for every car. After 11 cars, they raised a total of \$93.50. After 23 cars, they raised a total of \$195.50.
Table:
| number of cars | amount raised in dollars | |
|---|---|---|
| row 1 | 11 | 93.50 |
| row 2 | 23 | 195.50 |
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
If your teacher gives you the data card:
Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.
Ten people can dig five holes in three hours. If $n$ people digging at the same rate dig $m$ holes in $d$ hours:
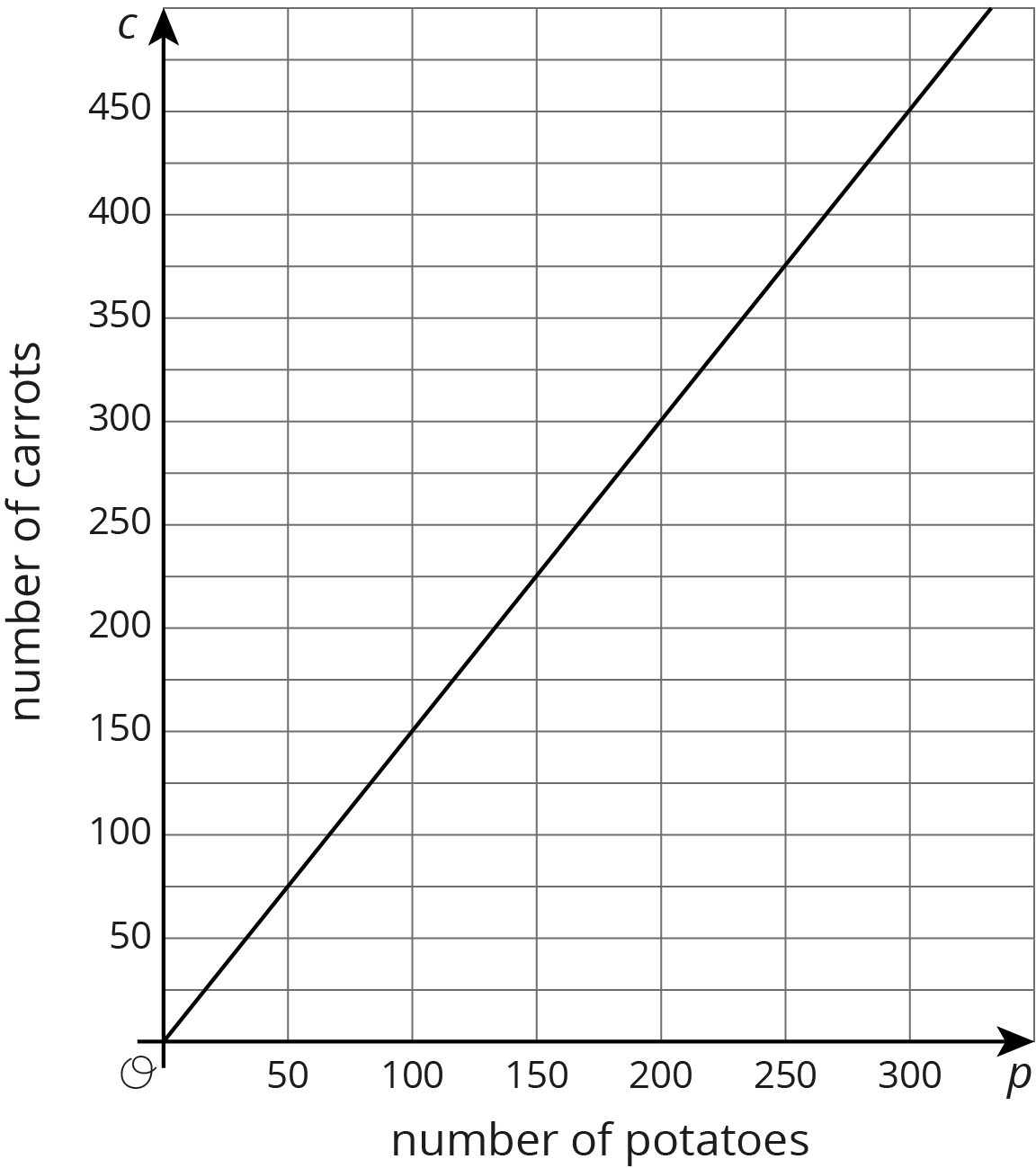
Proportional relationships can be represented in multiple ways. Which representation we choose depends on the purpose. And when we create representations we can choose helpful values by paying attention to the context. For example, a stew recipe calls for 3 carrots for every 2 potatoes. One way to represent this is using an equation. If there are $p$ potatoes and $c$ carrots, then $c = \frac32p$.
Suppose we want to make a large batch of this recipe for a family gathering, using 150 potatoes. To find the number of carrots we could just use the equation: $\frac32\boldcdot 150= 225$ carrots.
Or if the recipe is used in a food factory that produces very large quantities and the potatoes come in bags of 150, we might just make a table of values showing the number of carrots needed for different multiplies of 150.
| number of potatoes | number of carrots | |
|---|---|---|
| row 1 | 150 | 225 |
| row 2 | 300 | 450 |
| row 3 | 450 | 675 |
| row 4 | 600 | 900 |
No matter the representation or the scale used, the constant of proportionality, $\frac32$, is evident in each. In the equation it is the number we multiply $p$ by; in the graph, it is the slope; and in the table, it is the number we multiply values in the left column to get numbers in the right column. We can think of the constant of proportionality as a rate of change of $c$ with respect to $p$. In this case the rate of change is $\frac32$ carrots per potato.
In a linear relationship between two quantities $x$ and $y$, with equation $y = mx + b$, the constant $m$ is the rate of change. It tells you how much $y$ changes when $x$ changes by 1. It is also the slope of the graph of the relationship.