A system of equations is a set of 2 (or more) equations where the variables represent the same unknown values. For example, suppose that two different kinds of bamboo are planted at the same time. Plant A starts at 6 ft tall and grows at a constant rate of $\frac14$ foot each day. Plant B starts at 3 ft tall and grows at a constant rate of $\frac12$ foot each day. We can write equations $y = \frac14 x + 6$ for Plant A and $y = \frac12 x +3$ for Plant B, where $x$ represents the number of days after being planted, and $y$ represents height. We can write this system of equations.
$$ \begin{cases} y = \frac14 x + 6 \\ y = \frac12 x +3 \end{cases}$$
Solving a system of equations means to find the values of $x$ and $y$ that make both equations true at the same time. One way we have seen to find the solution to a system of equations is to graph both lines and find the intersection point. The intersection point represents the pair of $x$ and $y$ values that make both equations true. Here is a graph for the bamboo example:
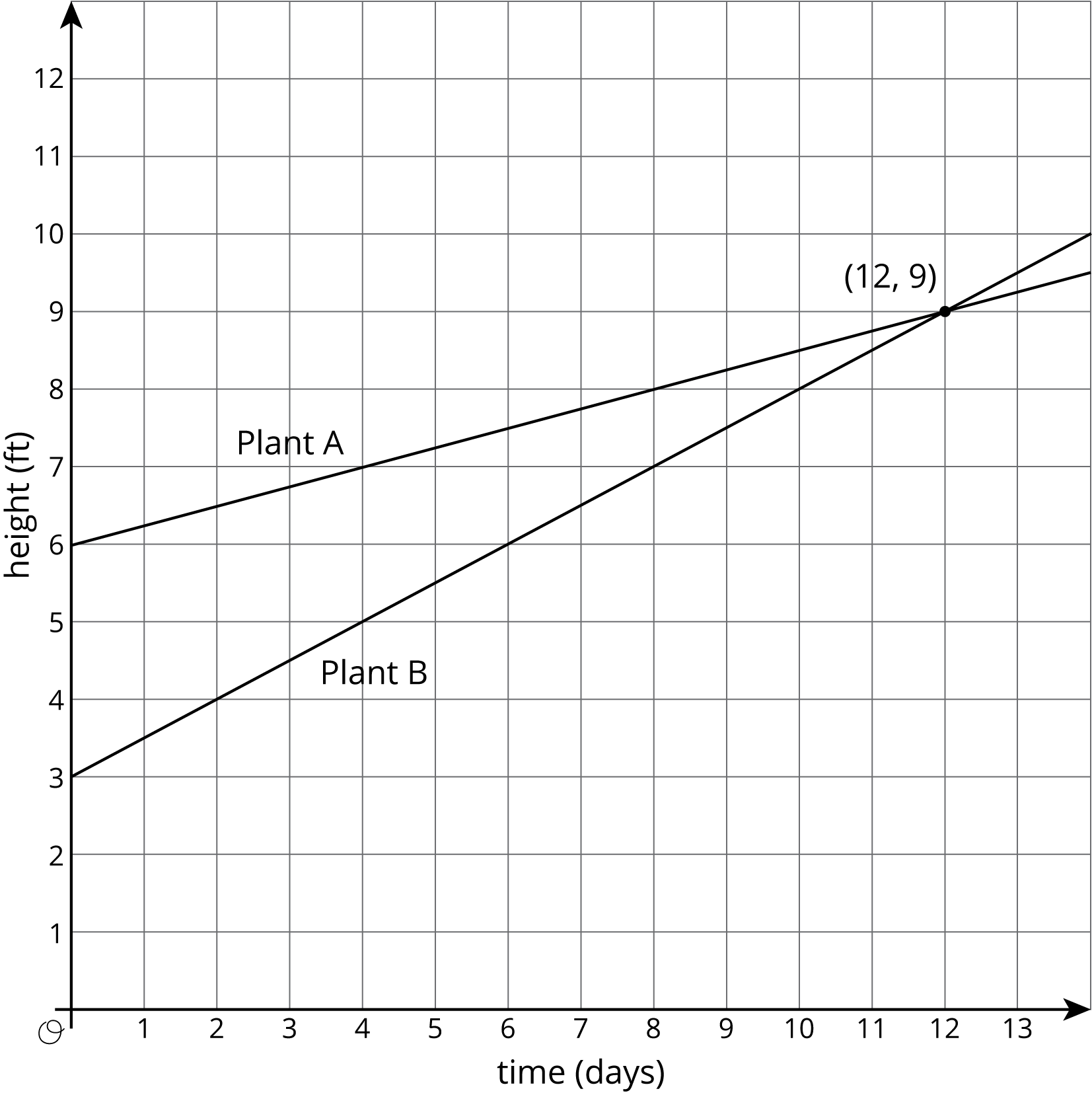
The solution to this system of equations is $(12,9)$, which means that both bamboo plants will be 9 feet tall after 12 days.
We have seen systems of equations that have no solutions, one solution, and infinitely many solutions.
- When the lines do not intersect, there is no solution. (Lines that do not intersect are parallel.)
- When the lines intersect once, there is one solution.
- When the lines are right on top of each other, there are infinitely many solutions.
In future lessons, we will see that some systems cannot be easily solved by graphing, but can be easily solved using algebra.
