Sometimes it is easier to solve a system of equations without having to graph the equations and look for an intersection point. In general, whenever we are solving a system of equations written as
$$\begin{cases} y = \text{[some stuff]}\\ y = \text{[some other stuff]} \end{cases}$$
we know that we are looking for a pair of values $(x,y)$ that makes both equations true. In particular, we know that the value for $y$ will be the same in both equations. That means that
$$\text{[some stuff]} = \text{[some other stuff]}$$
For example, look at this system of equations:
$$\begin{cases} y = 2x + 6 \\ y = \text-3x - 4 \end{cases}$$
Since the $y$ value of the solution is the same in both equations, then we know $$2x + 6 = \text-3x -4$$
We can solve this equation for $x$:
\(\begin{align} 2x + 6 &= \text-3x -4 \\ 5x + 6 &= \text-4 && \text{add $3x$ to each side} \\ 5x &= \text-10 && \text{subtract 6 from each side} \\ x &= \text-2 && \text{divide each side by 5} \end{align}\)
But this is only half of what we are looking for: we know the value for $x$, but we need the corresponding value for $y$. Since both equations have the same $y$ value, we can use either equation to find the $y$-value:
$$y = 2(\text-2) + 6$$
Or
$$y = \text-3(\text-2) -4$$
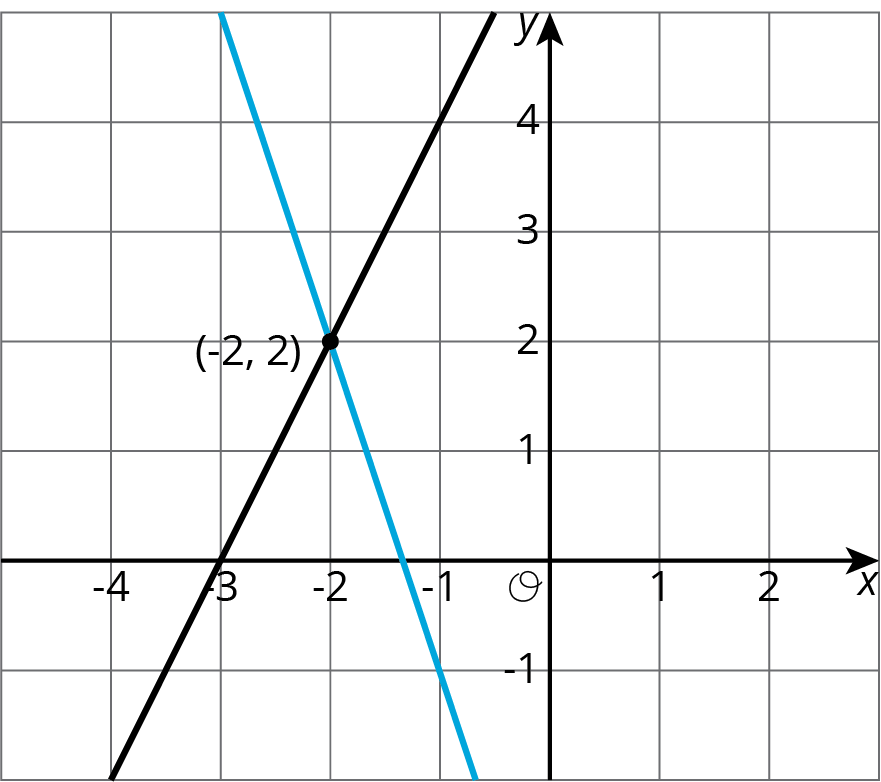
In both cases, we find that $y = 2$. So the solution to the system is $(\text-2,2)$. We can verify this by graphing both equations in the coordinate plane.
In general, a system of linear equations can have:
- No solutions. In this case, the lines that correspond to each equation never intersect.
- Exactly one solution. The lines that correspond to each equation intersect in exactly one point.
- An infinite number of solutions. The graphs of the two equations are the same line!