2.1: Notice and Wonder: Hanging Socks
What do you notice? What do you wonder?

Let's figure out unknown weights on balanced hangers.
What do you notice? What do you wonder?

This picture represents a hanger that is balanced because the weight on both sides is the same.
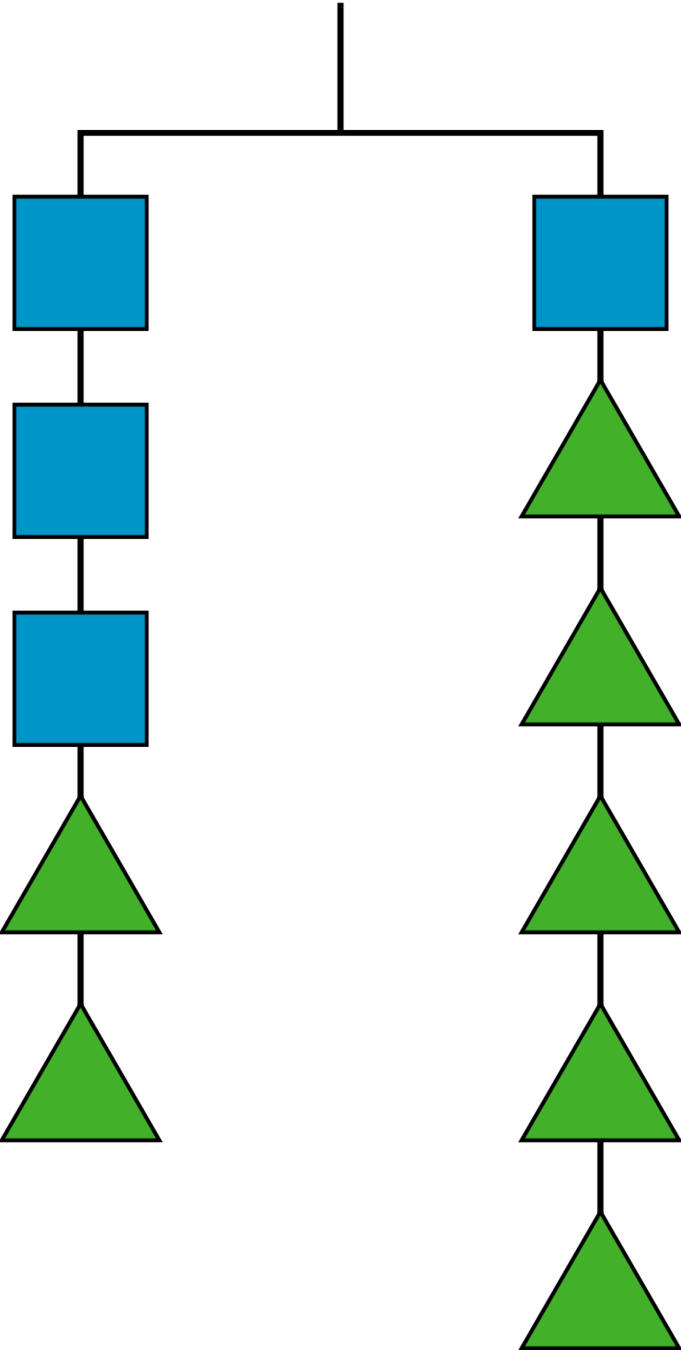
Elena takes two triangles off of the left side and three triangles off of the right side. Will the hanger still be in balance, or will it tip to one side? Which side? Explain how you know.
Use the applet to see if your answer to question [1] was correct. Can you find another way to make the hanger balance?
Try your own Hanger Balances!
Find the weight of a square.
A triangle weighs 3 grams, and a circle weighs 6 grams. Find the weight of a pentagon.
Write an equation to represent each hanger.
Try your own!
If we have equal weights on the ends of a hanger, then the hanger will be in balance. If there is more weight on one side than the other, the hanger will tilt to the heavier side.
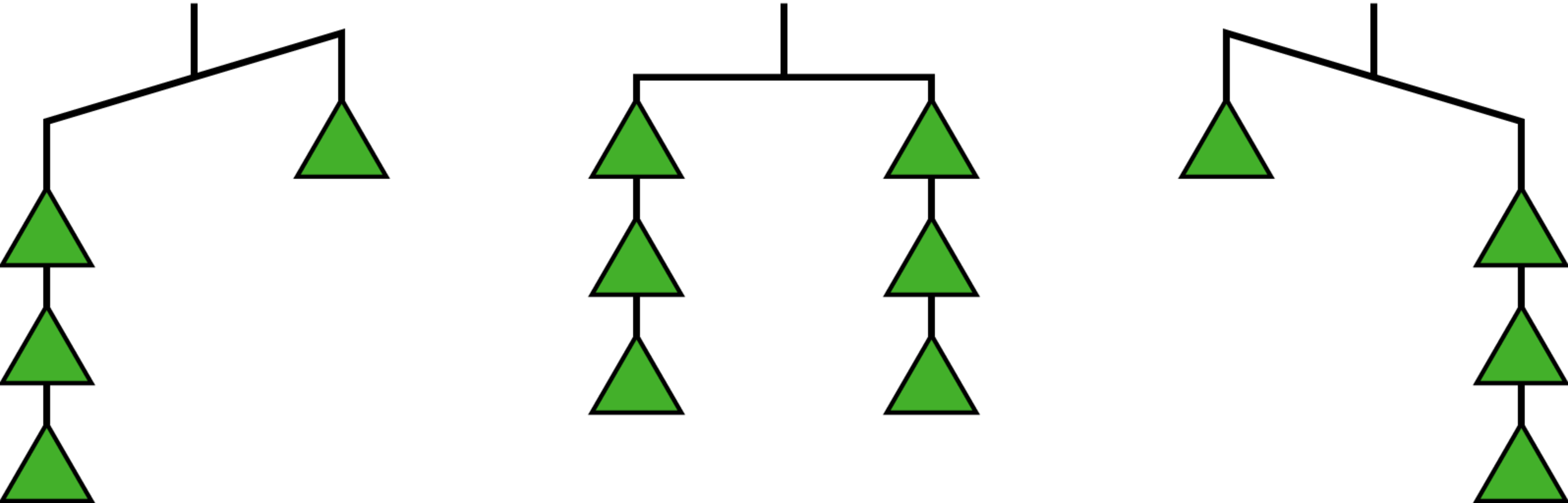
We can think of a balanced hanger as a metaphor for an equation. An equation says that the expressions on each side have equal value, just like a balanced hanger has equal weights on each side.
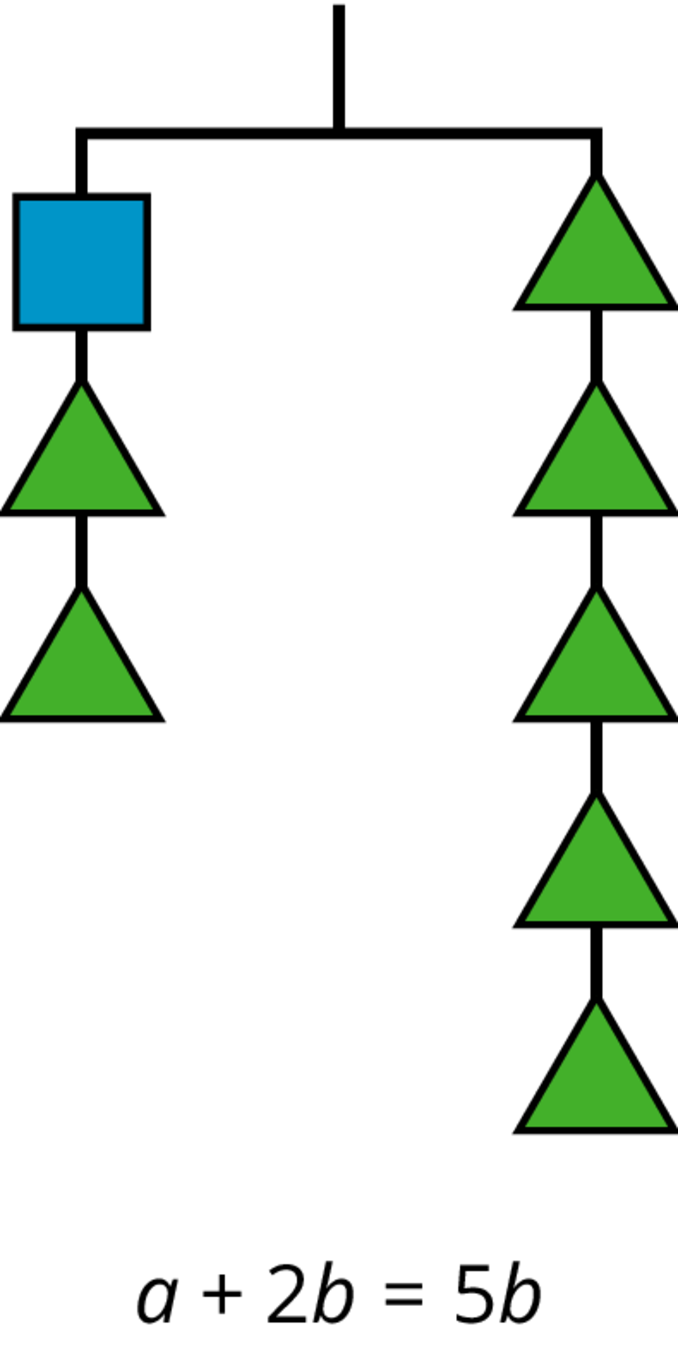
If we have a balanced hanger and add or remove the same amount of weight from each side, the result will still be in balance.
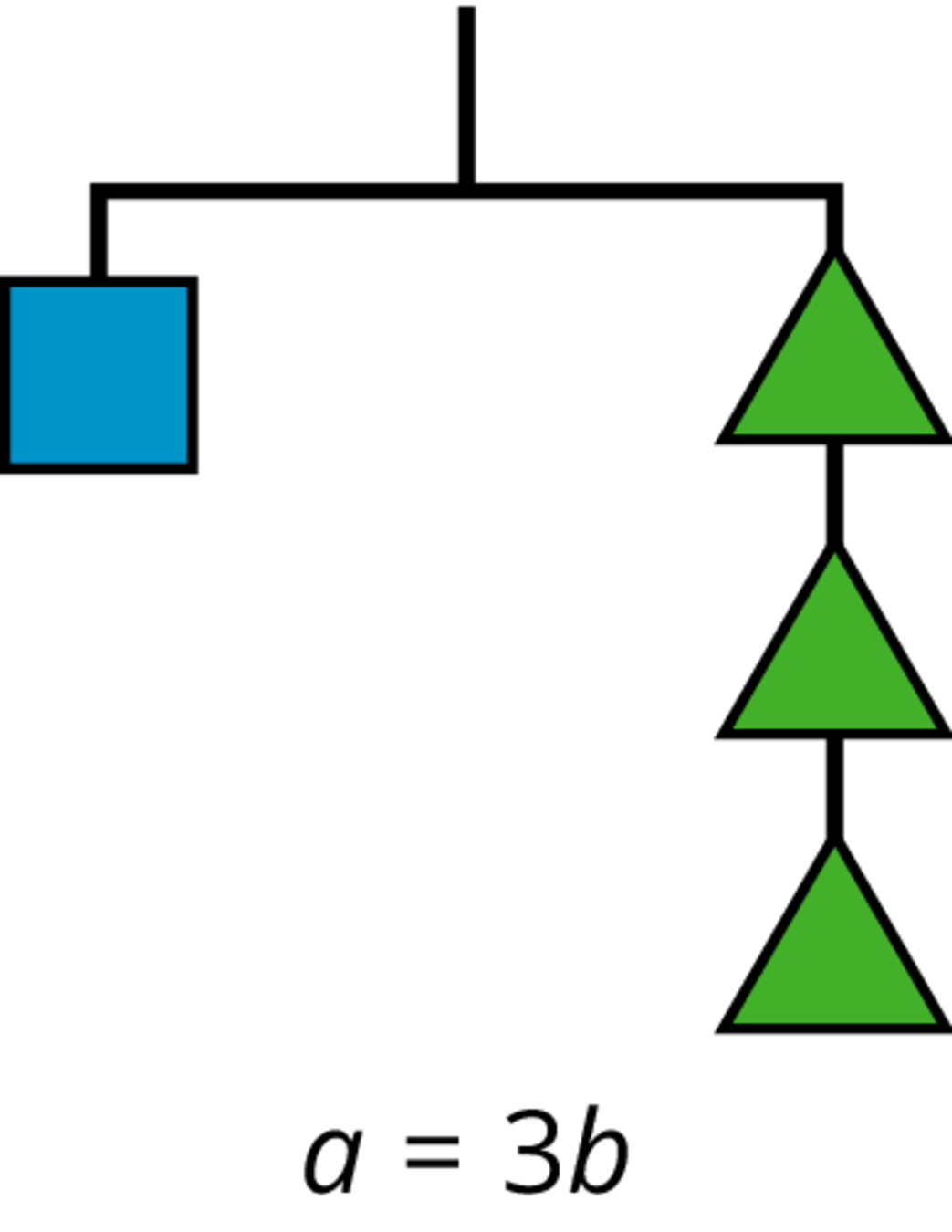
We can do these moves with equations as well: adding or subtracting the same amount from each side of an equation maintains the equality.