6.1: Equal Perimeters
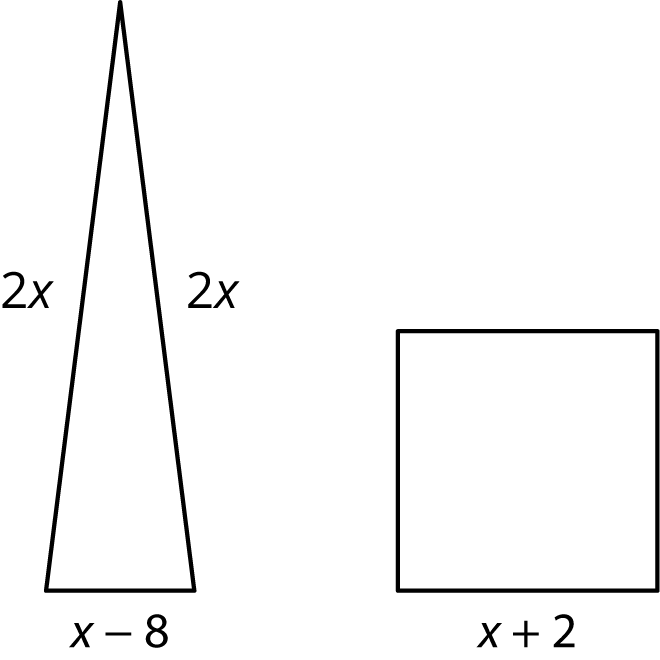
The triangle and the square have equal perimeters.
- Find the value of $x$.
- What is the perimeter of each of the figures?
Let's solve linear equations like a boss.
The triangle and the square have equal perimeters.

Without solving, identify whether these equations have a solution that is positive, negative, or zero.
Here are a lot of equations:
A. \(\text{-} \frac56(8+5b)=75+\frac53 b\)
B. \(\text-\frac12(t+3)-10=\text-6.5\)
C. \(\frac{10-v}{4}=2(v+17)\)
D. \(2(4k+3)-13=2(18-k)-13\)
E. \(\frac{n}{7}-12=5n+5\)
F. \(3(c-1)+2(3c+1)=\text-(3c+1)\)
G. \(\frac{4m-3}4=\text{-}\frac{9+4m}8\)
H. \(p-5(p+4)=p-(8-p)\)
I. \(2(2q+1.5)=18-q\)
J. \(2r+49=\text{-}8(\text{-}r-5)\)
Mai gave half of her brownies, and then half a brownie more, to Kiran. Then she gave half of what was left, and half a brownie more, to Tyler. That left her with one remaining brownie. How many brownies did she have to start with?
Sometimes we are asked to solve equations with a lot of things going on on each side. For example,
\(x-2(x+5)=\dfrac{3(2x-20)}{6}\)
This equation has variables on each side, parentheses, and even a fraction to think about. Before we start distributing, let's take a closer look at the fraction on the right side. The expression $2x-20$ is being multiplied by 3 and divided by 6, which is the same as just dividing by 2, so we can re-write the equation as
\(x-2(x+5)=\dfrac{2x-20}{2}\)
But now it’s easier to see that all the terms on the numerator of right side are divisible by 2, which means we can re-write the right side again as
\(x-2(x+5)=x-10\)
At this point, we could do some distribution and then collect like terms on each side of the equation. Another choice would be to use the structure of the equation. Both the left and the right side have something being subtracted from $x$. But, if the two sides are equal, that means the "something" being subtracted on each side must also be equal. Thinking this way, the equation can now be re-written with less terms as
\(2(x+5)=10\)
Only a few steps left! But what can we tell about the solution to this problem right now? Is it positive? Negative? Zero? Well, the 2 and the 5 multiplied together are 10, so that means the 2 and the $x$ multiplied together cannot have a positive or a negative value. Finishing the steps we have:
\(\begin{align} 2(x+5)&=10\\ x+5&=5&&\text{Divide each side by 2}\\ x &=0&&\text{Subtract 5 from each side}\\ \end{align}\)
Neither positive nor negative. Just as predicted.