Table A:
| input | output | |
|---|---|---|
| row 1 | -2 | 4 |
| row 2 | -1 | 1 |
| row 3 | 0 | 0 |
| row 4 | 1 | 1 |
| row 5 | 2 | 4 |
Given the rule:
 Complete the table for the function rule for the following input values:
Complete the table for the function rule for the following input values:
| input | 0 | 2 | 4 | 6 | 8 | 10 |
|---|---|---|---|---|---|---|
| output |
Here is an input-output rule:
 Complete the table for the input-output rule:
Complete the table for the input-output rule:
| input | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| output |
Andre’s school orders some new supplies for the chemistry lab. The online store shows a pack of 10 test tubes costs \$4 less than a set of nested beakers. In order to fully equip the lab, the school orders 12 sets of beakers and 8 packs of test tubes.
Solve: \(\begin{cases} y=x-4 \\ y=6x-10\\ \end{cases}\)
For what value of $x$ do the expressions $2x+3$ and $3x-6$ have the same value?
Here are several function rules. Calculate the output for each rule when you use -6 as the input.
A group of students is timed while sprinting 100 meters. Each student’s speed can be found by dividing 100 m by their time. Is each statement true or false? Explain your reasoning.
These tables correspond to inputs and outputs. Which of these input and output tables could represent a function rule, and which ones could not? Explain or show your reasoning.
Table A:
| input | output | |
|---|---|---|
| row 1 | -2 | 4 |
| row 2 | -1 | 1 |
| row 3 | 0 | 0 |
| row 4 | 1 | 1 |
| row 5 | 2 | 4 |
Table B:
| input | output | |
|---|---|---|
| row 1 | 4 | -2 |
| row 2 | 1 | -1 |
| row 3 | 0 | 0 |
| row 4 | 1 | 1 |
| row 5 | 4 | 2 |
Table C:
| input | output | |
|---|---|---|
| row 1 | 1 | 0 |
| row 2 | 2 | 0 |
| row 3 | 3 | 0 |
Table D:
| input | output | |
|---|---|---|
| row 1 | 0 | 1 |
| row 2 | 0 | 2 |
| row 3 | 0 | 3 |
Here is an equation that represents a function: $72x+12y=60$.
Select all the different equations that describe the same function:
$120y + 720x = 600$
$y = 5 - 6x$
$2y + 12x = 10$
$y = 5 + 6x$
$x=\frac{5}{6} - \frac{y}{6}$
$7x + 2y = 6$
$x=\frac{5}{6} + \frac{y}{6}$
Brown rice costs \$2 per pound, and beans cost \$1.60 per pound. Lin has \$10 to spend on these items to make a large meal of beans and rice for a potluck dinner. Let $b$ be the number of pounds of beans Lin buys and $r$ be the number of pounds of rice she buys when she spends all her money on this meal.
Solve each equation and check your answer.
The graph and the table show the high temperatures in a city over a 10-day period.

| day | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| temperature (degrees F) | 60 | 61 | 63 | 61 | 62 | 61 | 60 | 65 | 67 | 63 |
What was the high temperature on Day 7?
On which days was the high temperature 61 degrees?
Is the high temperature a function of the day? Explain how you know.
Is the day a function of the high temperature? Explain how you know.
The amount Lin’s sister earns at her part-time job is proportional to the number of hours she works. She earns \$9.60 per hour.
Write an equation in the form $y=kx$ to describe this situation, where $x$ represents the hours she works and $y$ represents the dollars she earns.
Is $y$ a function of $x$? Explain how you know.
Write an equation describing $x$ as a function of $y$.
Use the equation $2m+4s=16$ to complete the table, then graph the line using $s$ as the dependent variable.
| $m$ | 0 | -2 | ||
|---|---|---|---|---|
| $s$ | 3 | 0 |

Solve the system of equations: \(\begin{cases} y=7x+10 \\ y=\text-4x-23 \\ \end{cases}\)
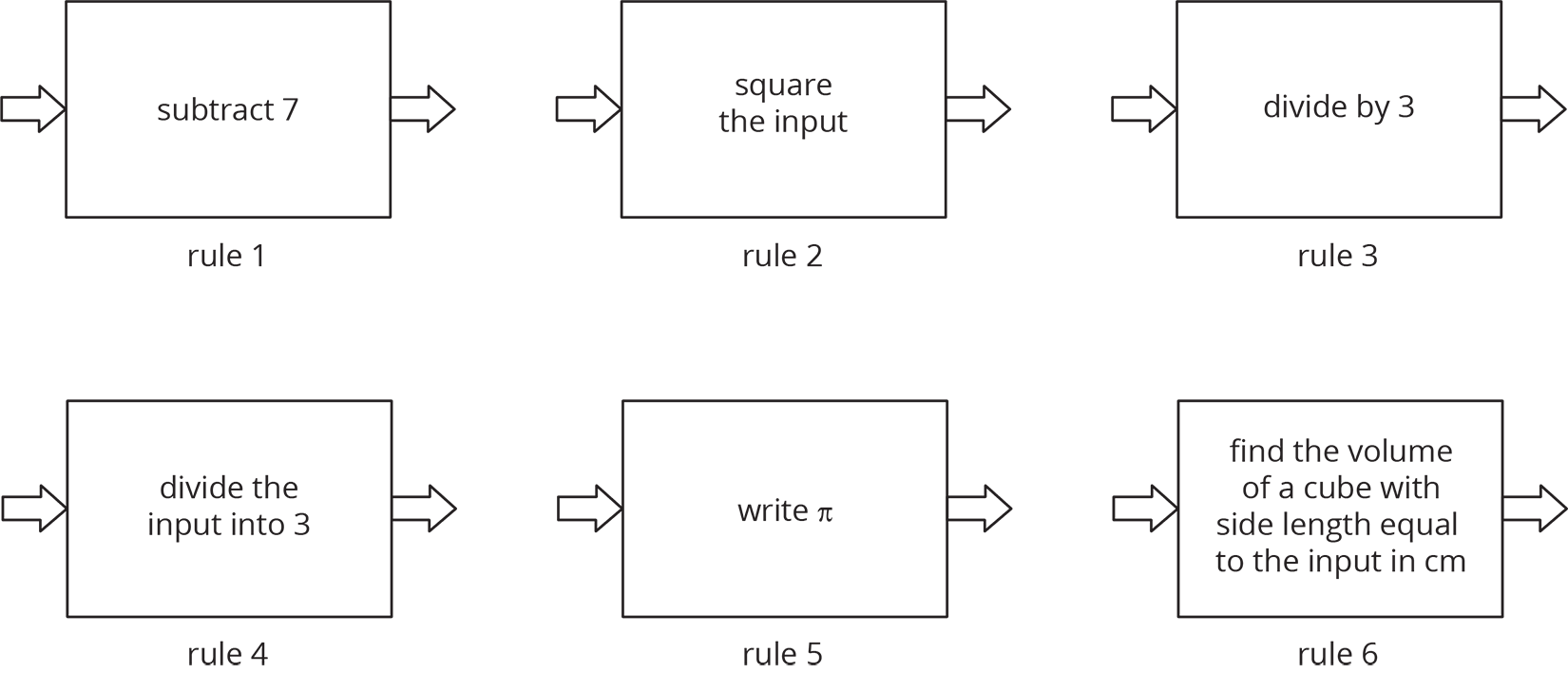
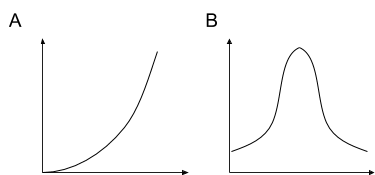
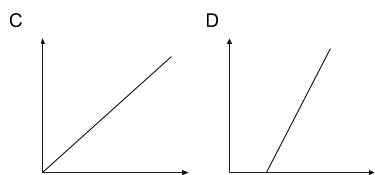
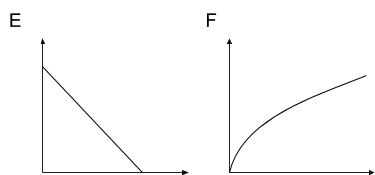
Match each diagram to the function described, then label the axes appropriately
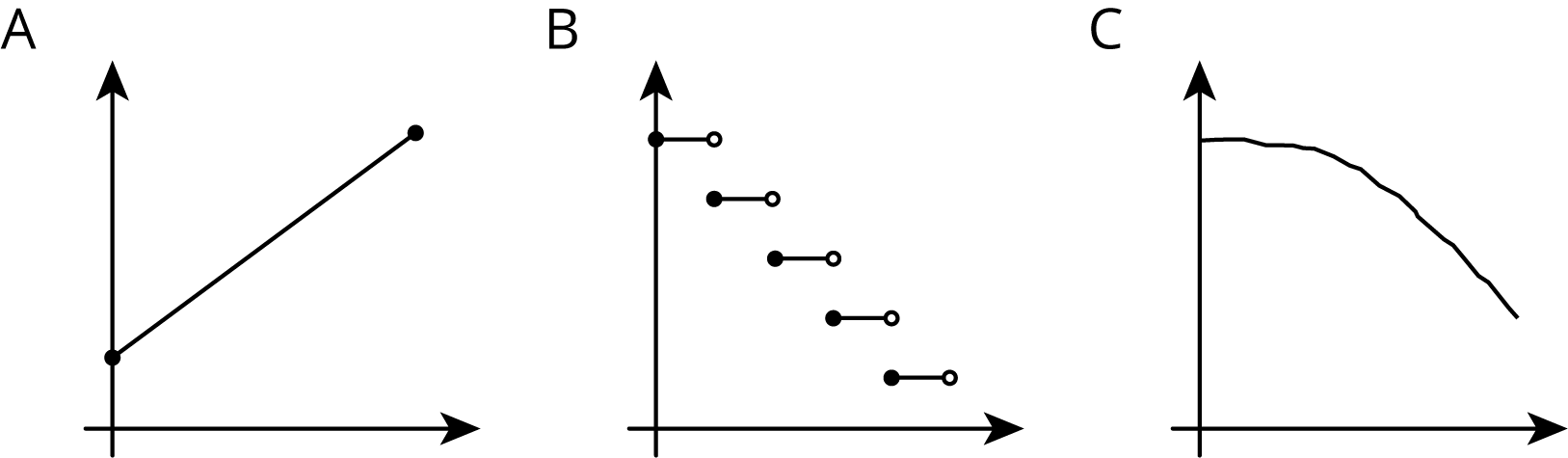
The solution to a system of equations is $(6,\text-3)$. Choose two equations that might make up the system.
A car is traveling on a small highway and is either going 55 miles per hour or 35 miles per hour, depending on the speed limits, until it reaches its destination 200 miles away. Letting $x$ represent the amount of time in hours that the car is going 55 miles per hour, and $y$ being the time in hours that the car is going 35 miles per hour, an equation describing the relationship is: $$55x + 35y = 200$$
The graph represents an object that is shot upwards from a tower and then falls to the ground. The independent variable is time in seconds and the dependent variable is the object’s height above the ground in meters.

Match the graph to the following situations (you can use a graph multiple times). For each match, name possible independent and dependent variables and how you would label the axes.
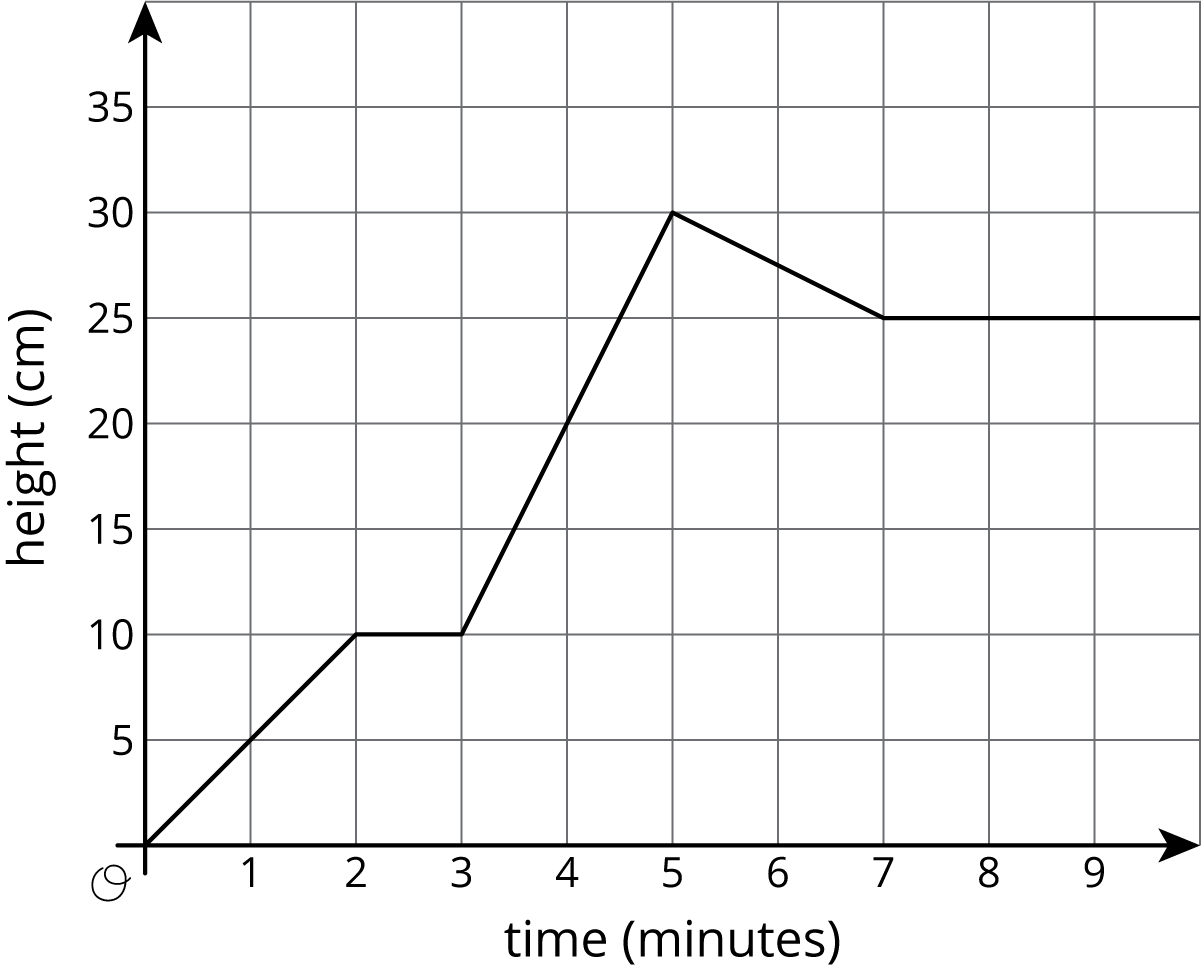
Jada fills her aquarium with water.
The graph shows the height of the water, in cm, in the aquarium as a function of time in minutes. Invent a story of how Jada fills the aquarium that fits the graph.
Recall the formula for area of a circle.
| $r$ | 3 | $\frac12$ | ||
|---|---|---|---|---|
| $A$ | $16\pi$ | $100\pi$ |
The points with coordinates $(4,8)$, $(2,10)$, and $(5,7)$ all lie on the line $2x+2y=24$.

The equation and the tables represent two different functions. Use the equation $b=4a-5$ and the table to answer the questions. This table represents $c$ as a function of $a$.
| $a$ | -3 | 0 | 2 | 5 | 10 | 12 |
|---|---|---|---|---|---|---|
| $c$ | -20 | 7 | 3 | 21 | 19 | 45 |
Match each function rule with the value that could not be a possible input for that function.
Elena and Lin are training for a race. Elena runs her mile a constant speed of 7.5 miles per hour.
Lin’s times are recorded every minute:
| time (minutes) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| distance (miles) | 0.11 | 0.21 | 0.32 | 0.41 | 0.53 | 0.62 | 0.73 | 0.85 | 1 |
Who finished their mile first?
This is a graph of Lin’s progress. Draw a graph to represent Elena’s mile on the same axes.

For these models, is distance a function of time? Is time a function of distance? Explain how you know.
Find a value of $x$ that makes the equation true: $$\text-(\text-2x+1)= 9-14x$$ Explain your reasoning, and check that your answer is correct.
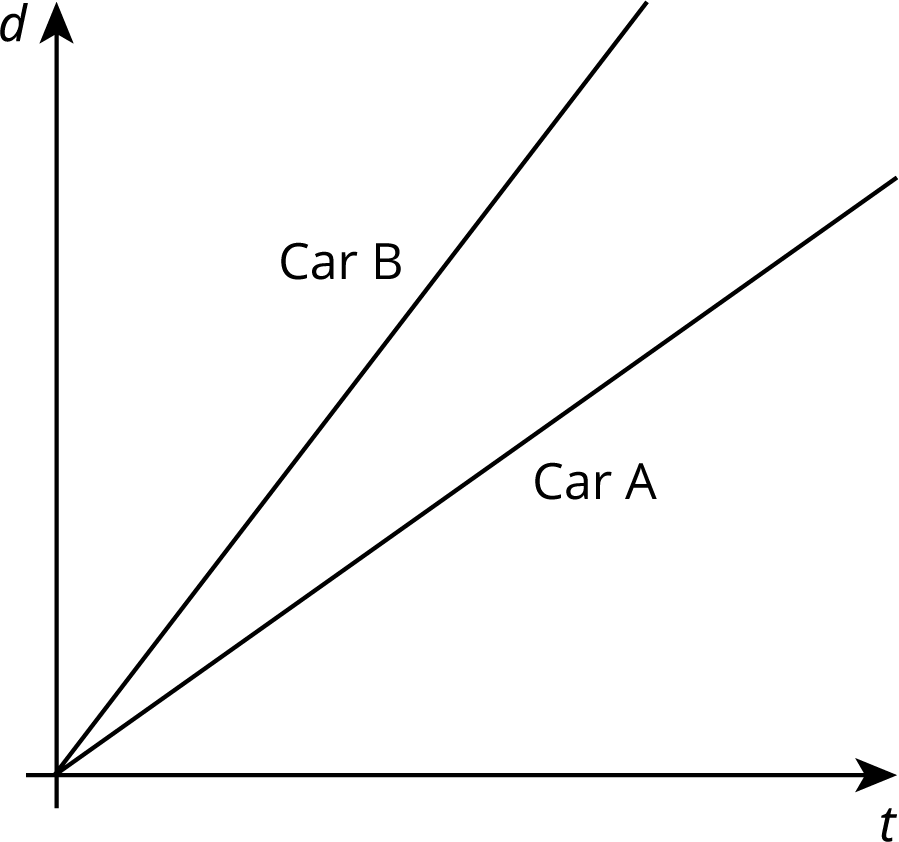
Two cars drive on the same highway in the same direction. The graphs show the distance, $d$, of each one as a function of time, $t$. Which car drives faster? Explain how you know.
Two car services offer to pick you up and take you to your destination. Service A charges 40 cents to pick you up and 30 cents for each mile of your trip. Service B charges \$1.10 to pick you up and charges $c$ cents for each mile of your trip.
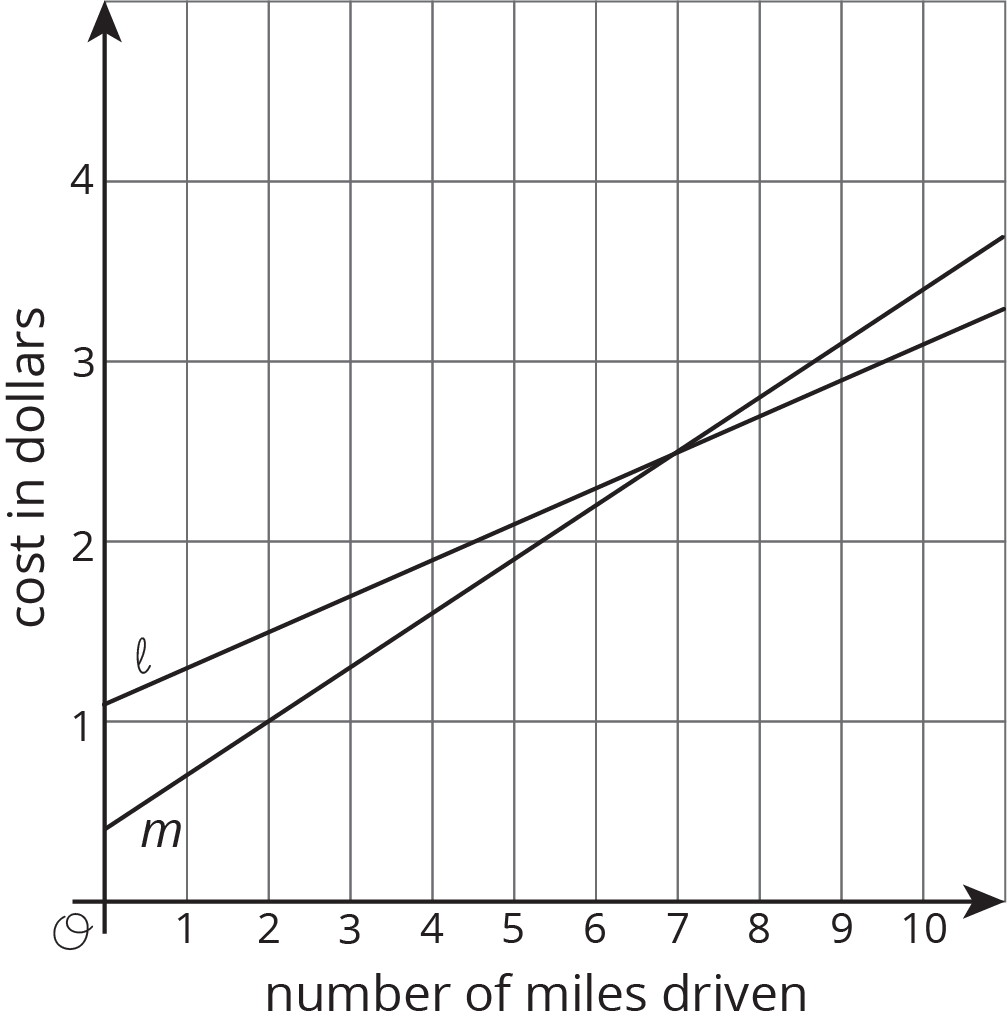
Kiran and Clare like to race each other home from school. They run at the same speed, but Kiran's house is slightly closer to school than Clare's house. On a graph, their distance from their homes in meters is a function of the time from when they begin the race in seconds.
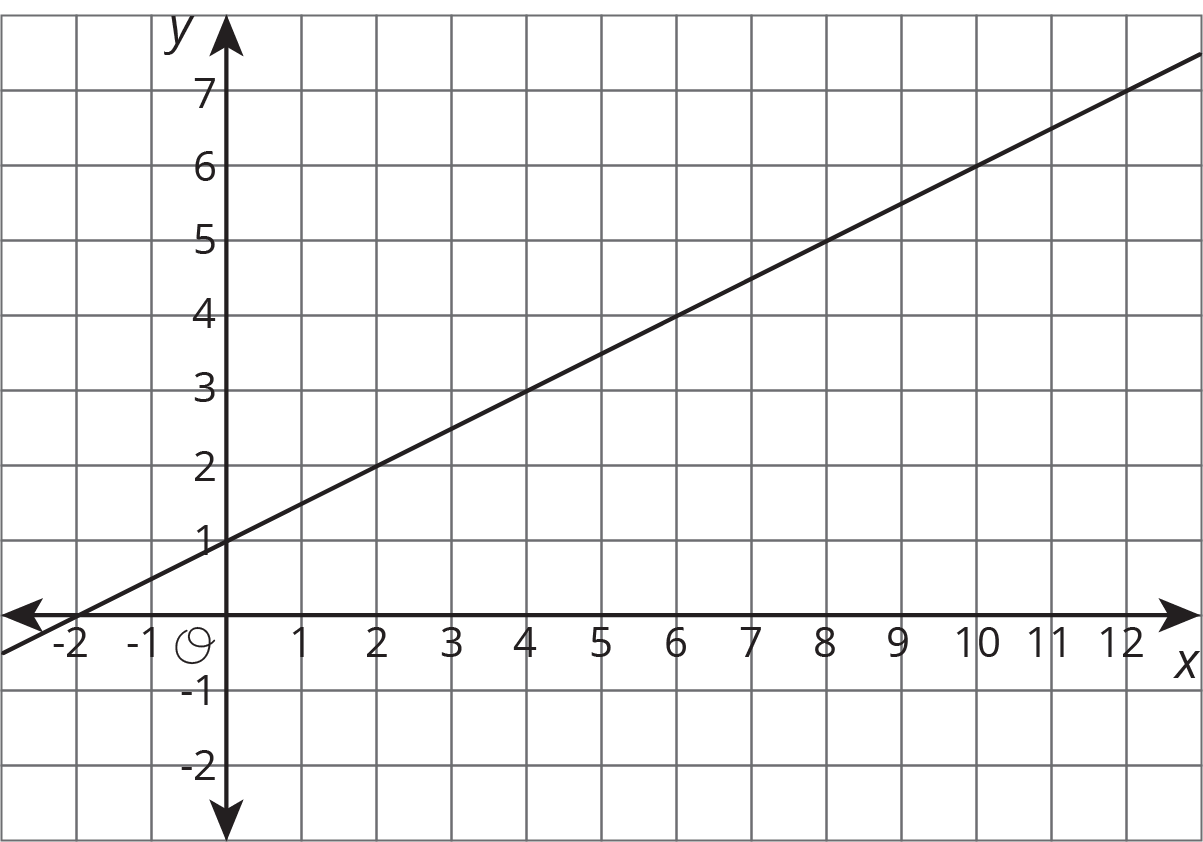
Write an equation for each line. 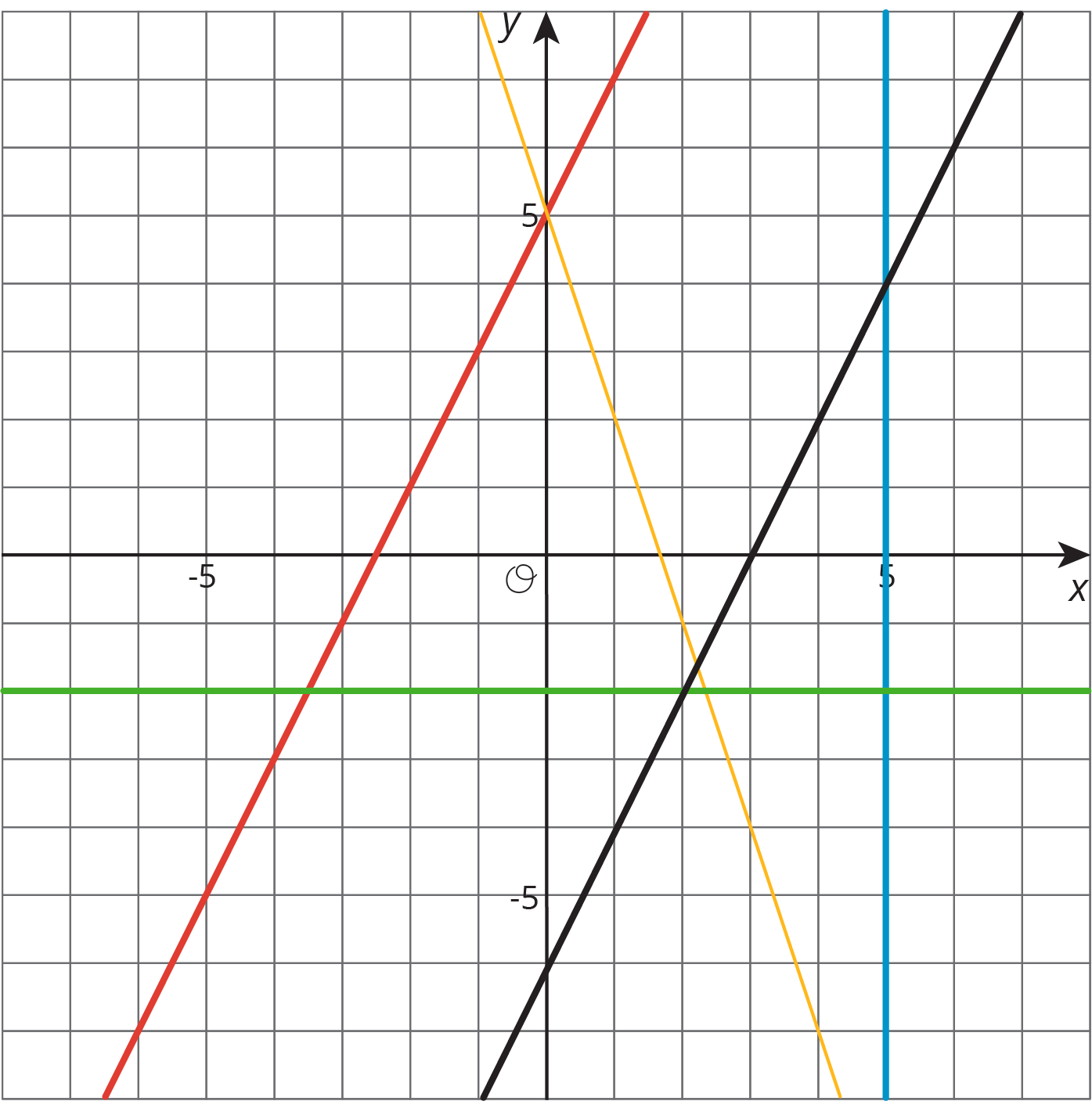
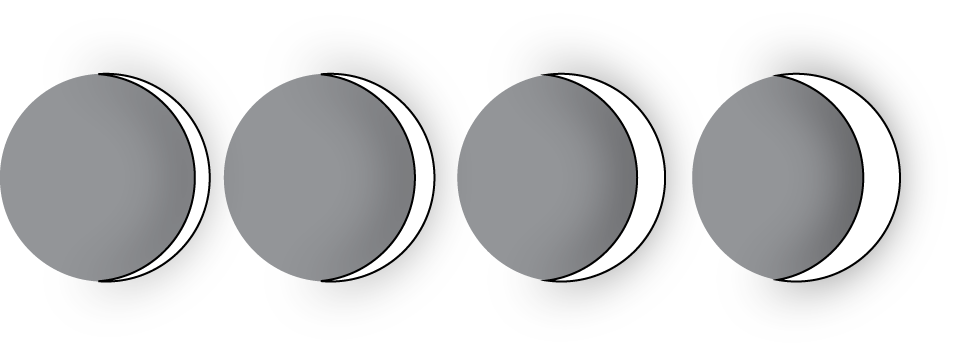
On the first day after the new moon, 2% of the moon's surface is illuminated. On the second day, 6% is illuminated.
Based on this information, predict the day on which the moon's surface is 50% illuminated and 100% illuminated.
The moon's surface is 100% illuminated on day 14. Does this agree with the prediction you made?
Is the percentage illumination of the moon's surface a linear function of the day?
In science class, Jada uses a graduated cylinder with water in it to measure the volume of some marbles. After dropping in 4 marbles so they are all under water, the water in the cylinder is at a height of 10 milliliters. After dropping in 6 marbles so they are all under water, the water in the cylinder is at a height of 11 milliliters.
Solve each of these equations. Explain or show your reasoning.
$2(3x+2)=2x+28$
$5y+13=\text-43-3y$
$4(2a+2)=8(2-3a)$
For a certain city, the high temperatures (in degrees Celsius) are plotted against the number of days after the new year.
 Based on this information, is the high temperature in this city a linear function of the number of days after the new year?
Based on this information, is the high temperature in this city a linear function of the number of days after the new year?
The school designed their vegetable garden to have a perimeter of 32 feet with the length measuring two feet more than twice the width.
Using $\ell$ to represent the length of the garden and $w$ to represent its width, write and solve a system of equations that describes this situation.
What are the dimensions of the garden?
The graph shows the distance of a car from home as a function of time.
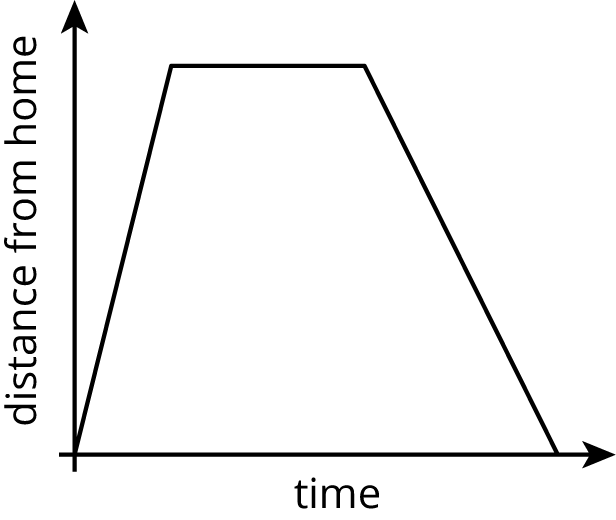
Describe what a person watching the car may be seeing.
The equation and the graph represent two functions. Use the equation $y=4$ and the graph to answer the questions.
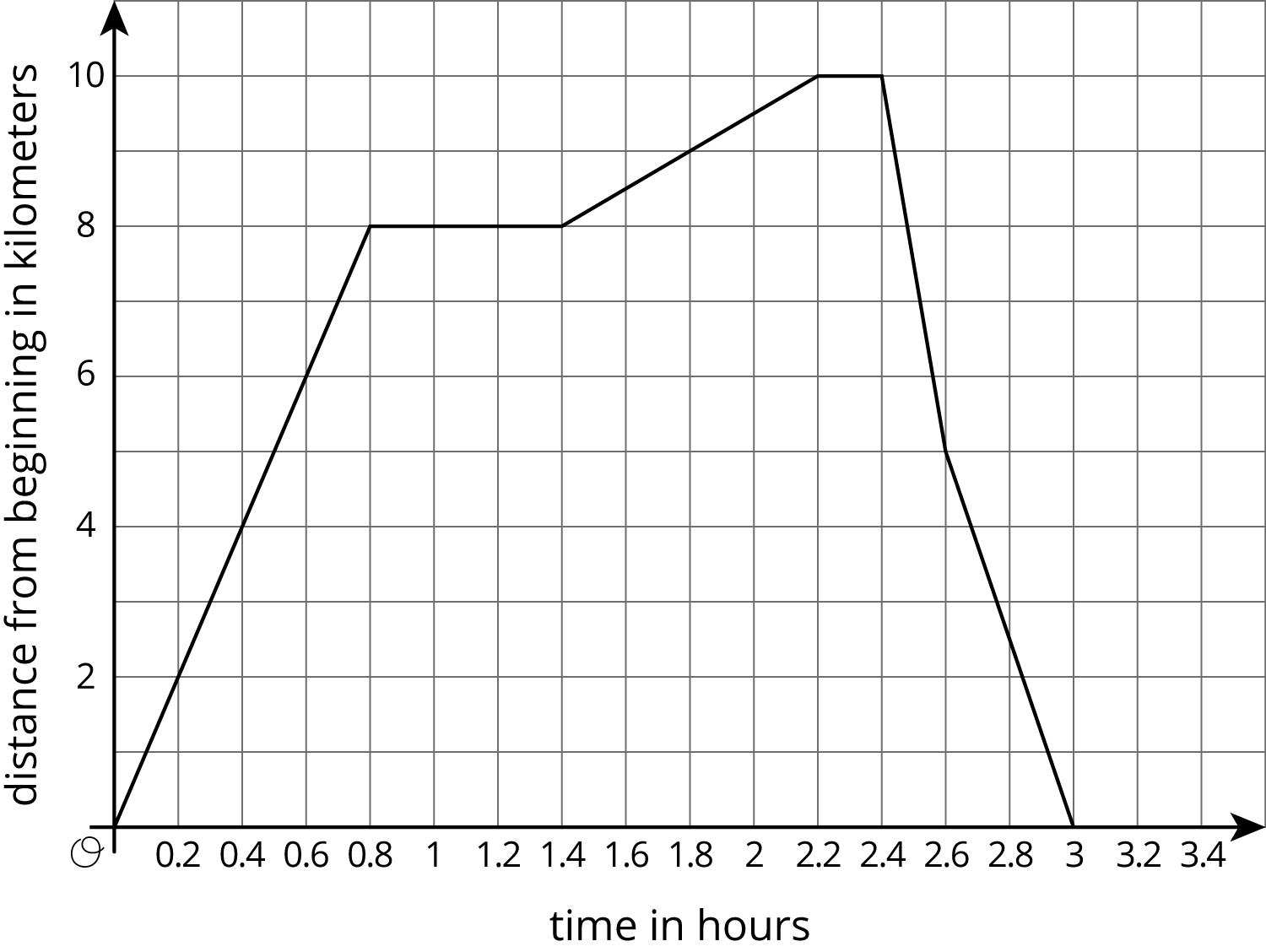
This graph shows a trip on a bike trail. The trail has markers every 0.5 km showing the distance from the beginning of the trail.
When was the bike rider going the fastest?
When was the bike rider going the slowest?
During what times was the rider going away from the beginning of the trail?
During what times was the rider going back towards the beginning of the trail?
During what times did the rider stop?
The expression $\text-25t+1250$ represents the volume of liquid of a container after $t$ seconds. The expression $50t+250$ represents the volume of liquid of another container after $t$ seconds. What does the equation $\text-25t+1250=50t+250$ mean in this situation?
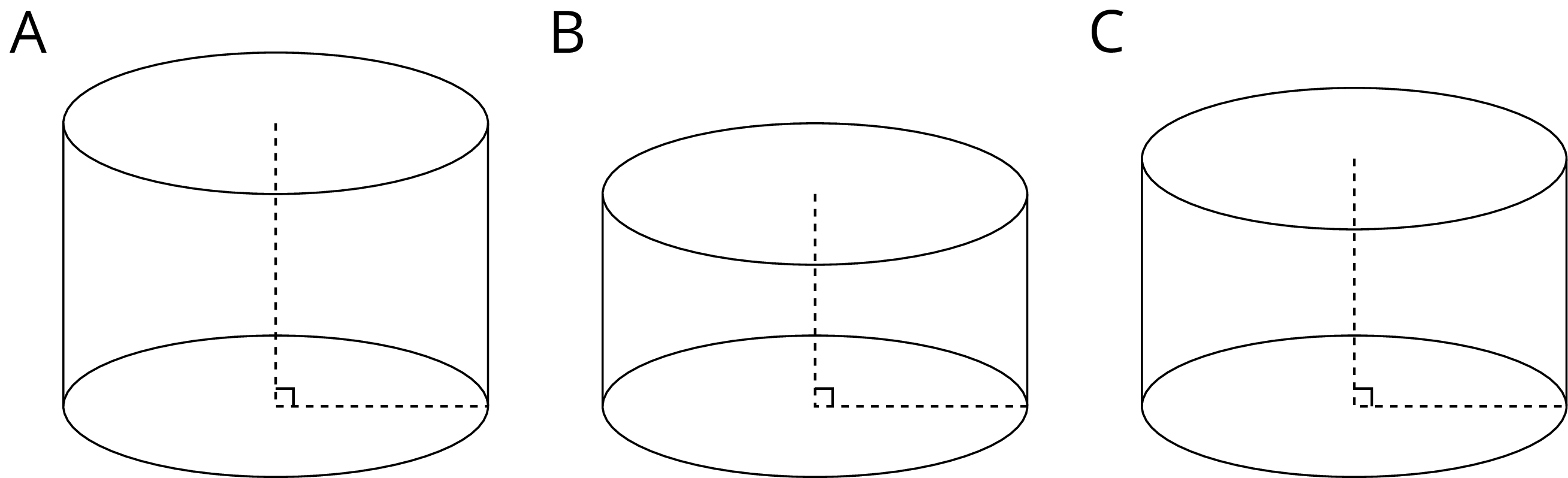
Cylinder A, B, and C have the same radius but different heights. Put the cylinders in order of their volume from least to greatest.
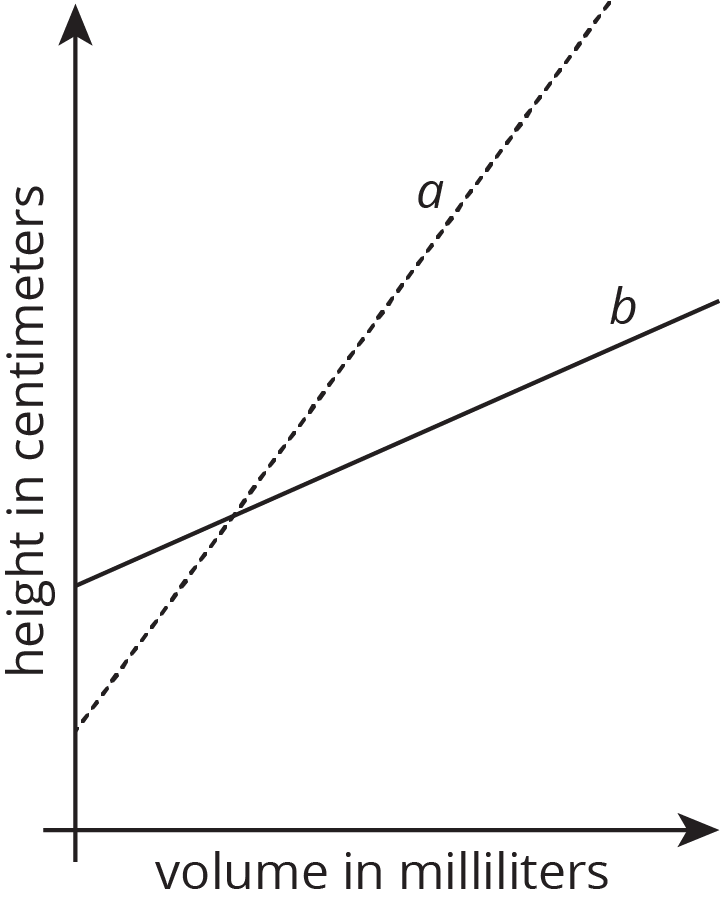
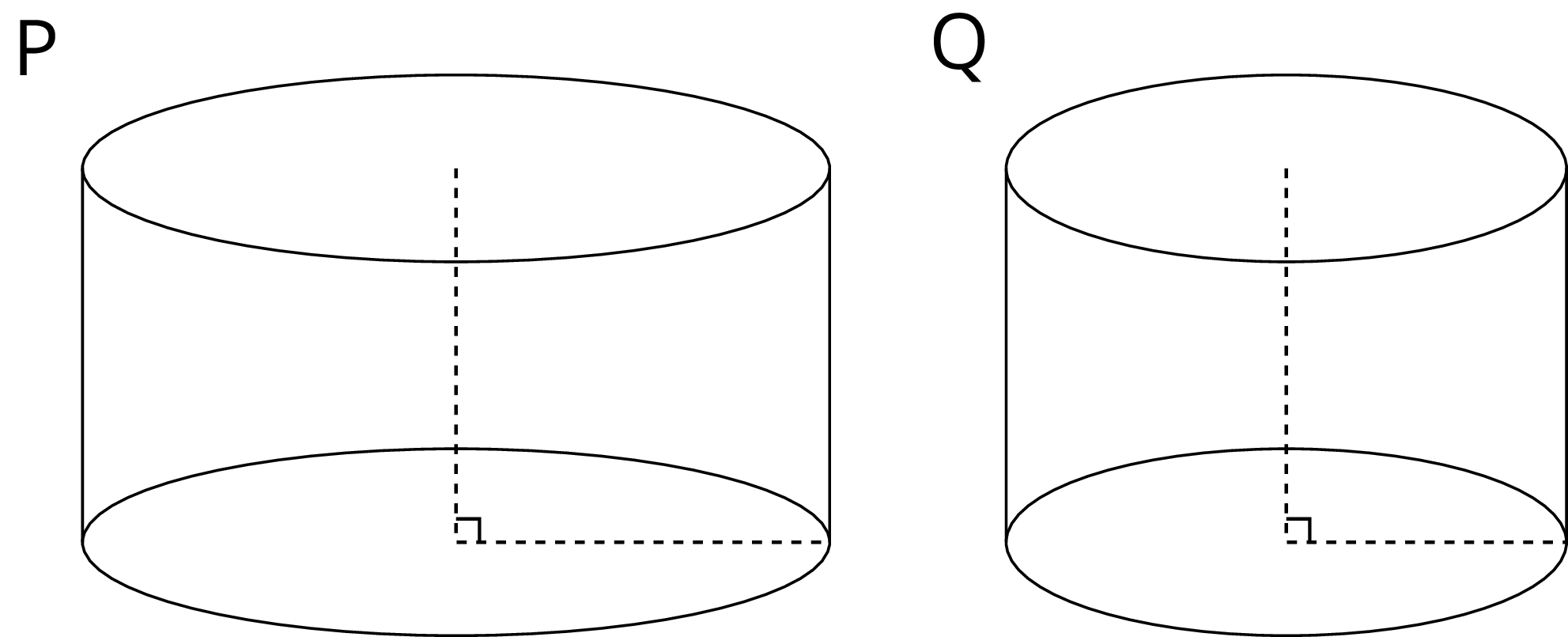
Two cylinders, $a$ and $b$, each started with different amounts of water. The graph shows how the height of the water changed as the volume of water increased in each cylinder. Match the graphs of $a$ and $b$ to Cylinders P and Q. Explain your reasoning.
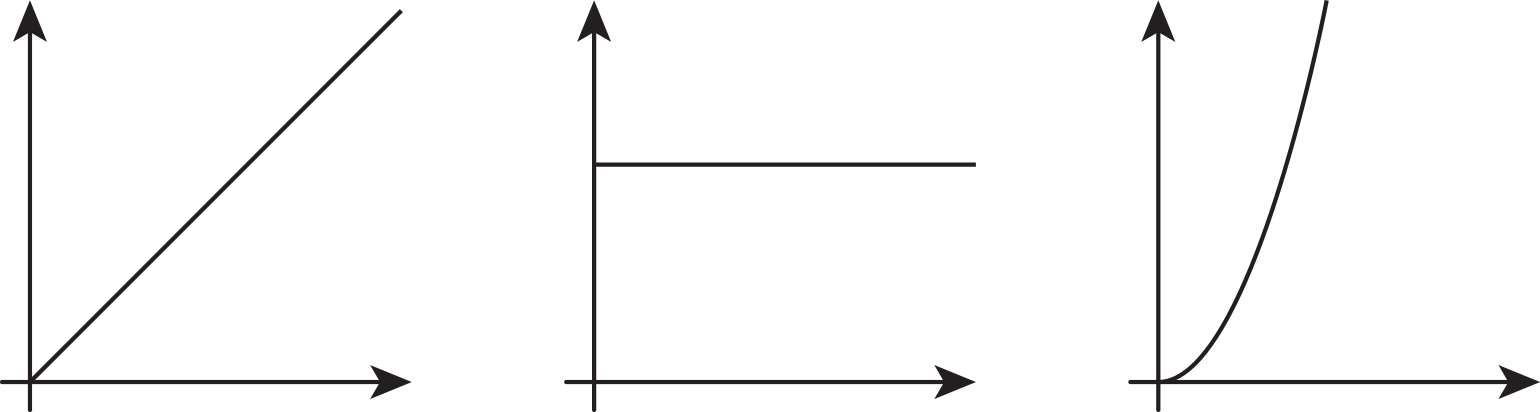
Which of the following graphs could represent the volume of water in a cylinder as a function of its height? Explain your reasoning.
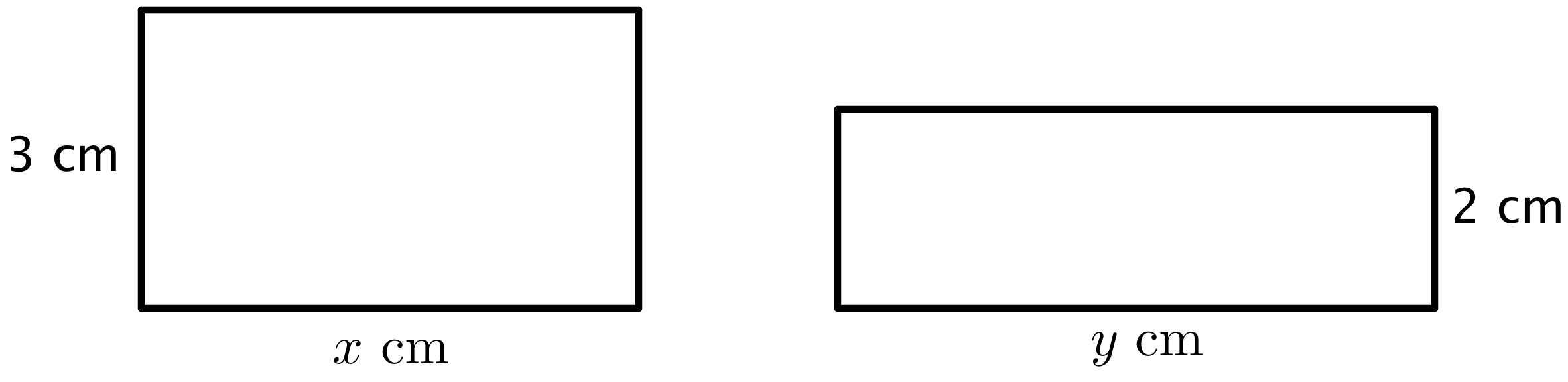
Together, the areas of the rectangles sum to 30 square centimeters.
| $x$ | 3 | 8 | 12 | ||
|---|---|---|---|---|---|
| $y$ | 5 | 10 |
Several glass aquariums of various sizes are for sale at a pet shop. They are all shaped like rectangular prisms. A 15-gallon tank is 24 inches long, 12 inches wide, and 12 inches tall. Match the dimensions of the other tanks with the volume of water they can each hold.
Two paper drink cups are shaped like cones. The small cone can hold 6 oz of water. The large cone is $\frac43$ the height and $\frac43$ the diameter of the small cone. Which of these could be the amount of water the large cone holds?
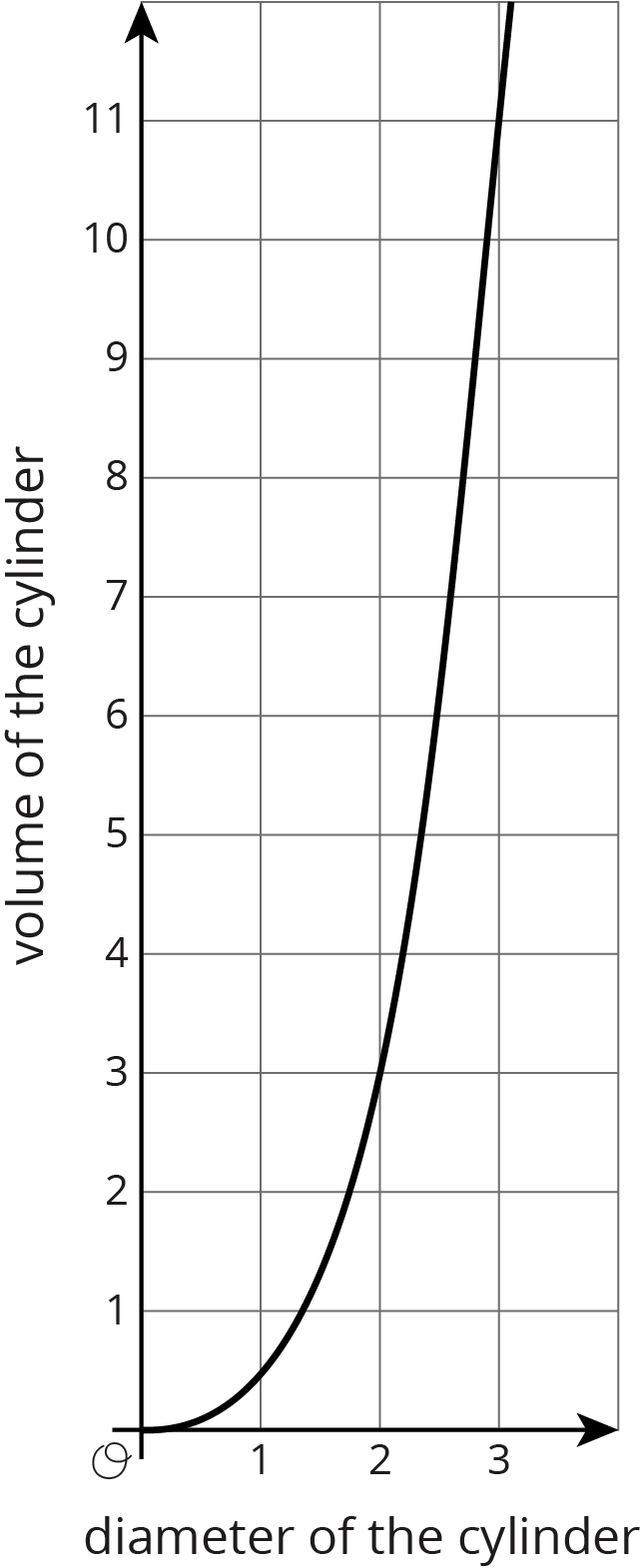
The graph represents the volume of a cylinder with a height equal to its radius.
Select all the points that are on a line with slope 2 that also contains the point $(2, \text-1)$.
Solve: \(\begin{cases} y=\text-2x-20 \\ y=x+4 \\ \end{cases}\)
Match each set of information about a circle with the area of that circle.
At a farm, animals are fed bales of hay and buckets of grain. Each bale of hay is in the shape a rectangular prism. The base has side lengths 2 feet and 3 feet, and the height is 5 feet. Each bucket of grain is a cylinder with a diameter of 3 feet. The height of the bucket is 5 feet, the same as the height of the bale.
Which is larger in area, the rectangular base of the bale or the circular base of the bucket? Explain how you know.
Which is larger in volume, the bale or the bucket? Explain how you know.
Three cylinders have a height of 8 cm. Cylinder 1 has a radius of 1 cm. Cylinder 2 has a radius of 2 cm. Cylinder 3 has a radius of 3 cm. Find the volume of each cylinder.
A one-quart container of tomato soup is shaped like a rectangular prism. A soup bowl shaped like a hemisphere can hold 8 oz of liquid. How many bowls will the soup container fill? Recall that 1 quart is equivalent to 32 fluid ounces (oz).
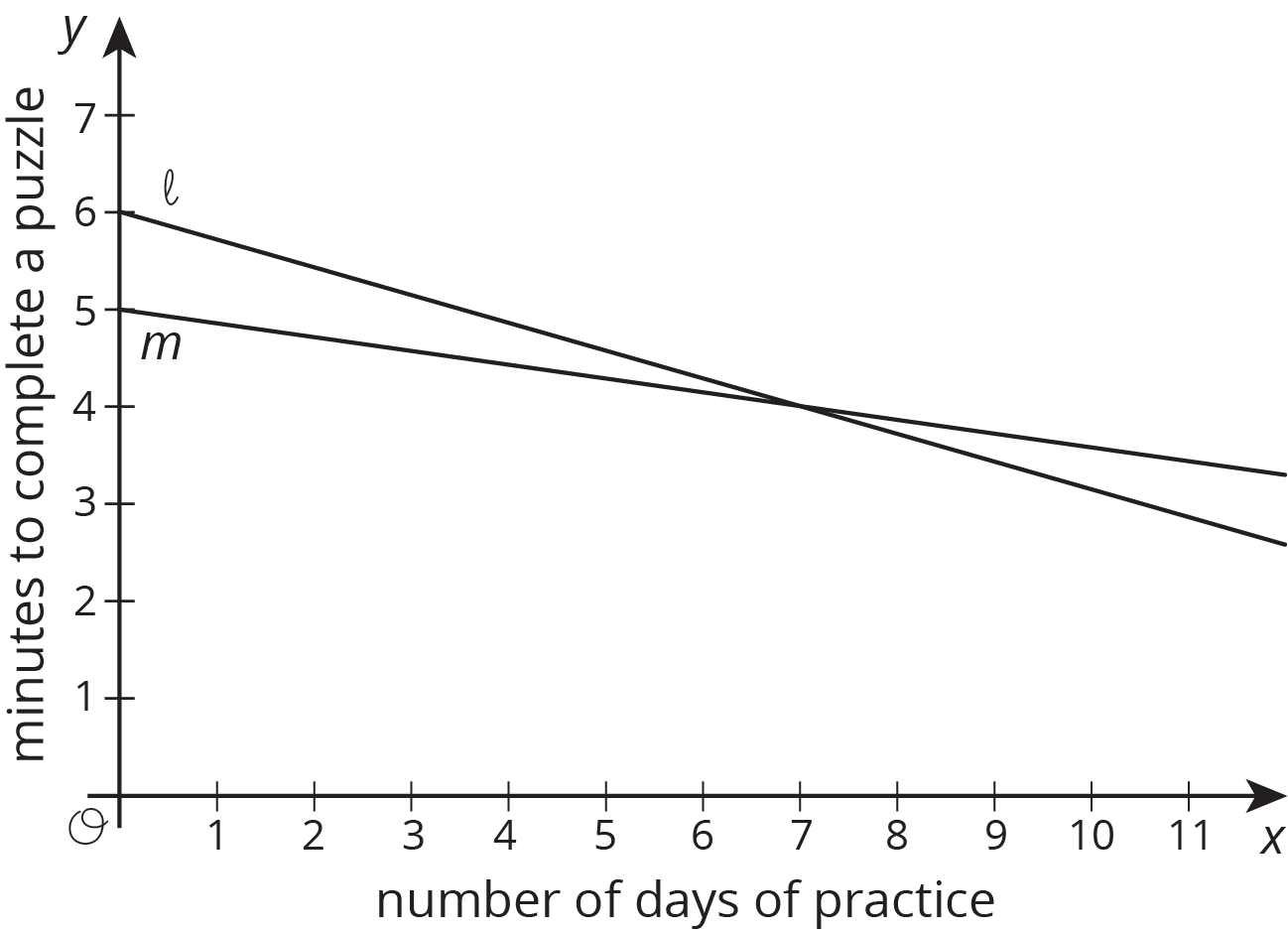
Two students join a puzzle solving club and get faster at finishing the puzzles as they get more practice. Student A improves their times faster than Student B.
Complete the table with all of the missing information about three different cylinders.
| diameter of base (units) | area of base (square units) | height (units) | volume (cubic units) | |
|---|---|---|---|---|
| row 1 | 4 | 10 | ||
| row 2 | 6 | $63 \pi$ | ||
| row 3 | $25 \pi$ | 6 |
A cylinder has volume $45\pi$ and radius 3. What is its height?
Three cylinders have a volume of 2826 cm3. Cylinder A has a height of 900 cm. Cylinder B has a height of 225 cm. Cylinder C has a height of 100 cm. Find the radius of each cylinder. Use 3.14 as an approximation for $\pi$.
A gas company’s delivery truck has a cylindrical tank that is 14 feet in diameter and 40 feet long.
Sketch the tank, and mark the radius and the height.
How much gas can fit in the tank?
Here is a graph that shows the water height of the ocean between September 22 and September 24, 2016 in Bodega Bay, CA.

Estimate the water height at 12 p.m. on September 22.
How many times was the water height 5 feet? Find two times when this happens.
What was the lowest the water got during this time period? When does this occur?
Does the water ever reach a height of 6 feet?
A cylinder and cone have the same height and radius. The height of each is 5 cm, and the radius is 2 cm. Calculate the volume of the cylinder and the cone.
The volume of this cone is $36\pi$ cubic units.
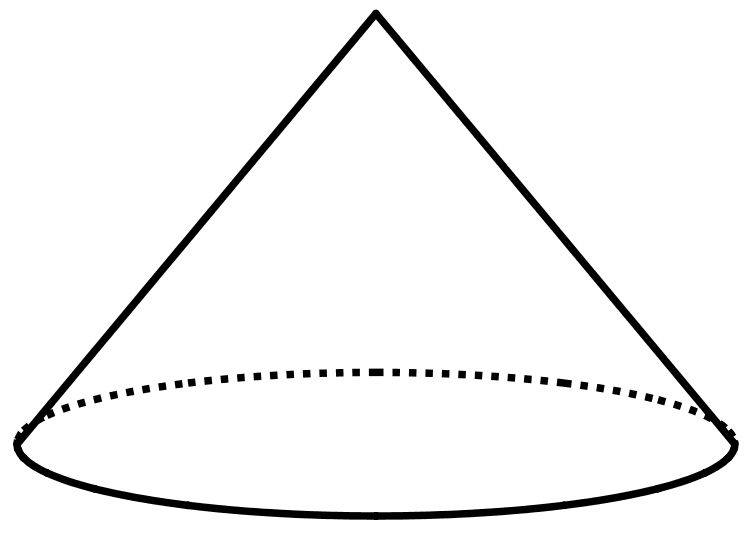
What is the volume of a cylinder that has the same base area and the same height?
A cylinder has a diameter of 6 cm and a volume of $36\pi$ cm3.
Lin wants to get some custom T-shirts printed for her basketball team. Shirts cost \$10 each if you order 10 or fewer shirts and \$9 each if you order 11 or more shirts.
Make a graph that shows the total cost of buying shirts, for 0 through 15 shirts.
There are 10 people on the team. Do they save money if they buy an extra shirt? Explain your reasoning.
What is the slope of the graph between 0 and 10? What does it mean in the story?
What is the slope of the graph between 11 and 15? What does it mean in the story?
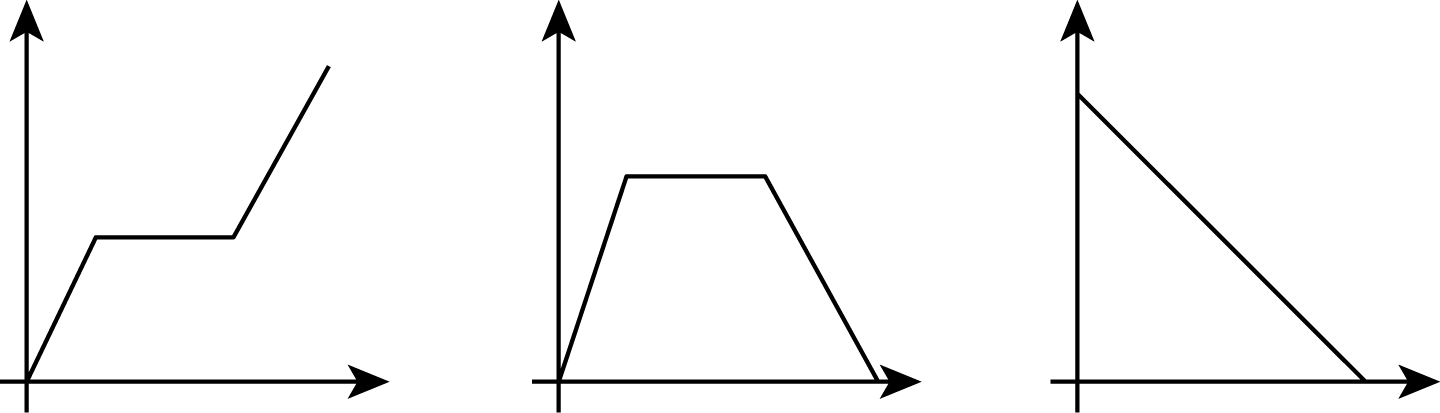
In the following graphs, the horizontal axis represents time and the vertical axis represents distance from school. Write a possible story for each graph.
The volume of this cylinder is $175\pi$ cubic units.
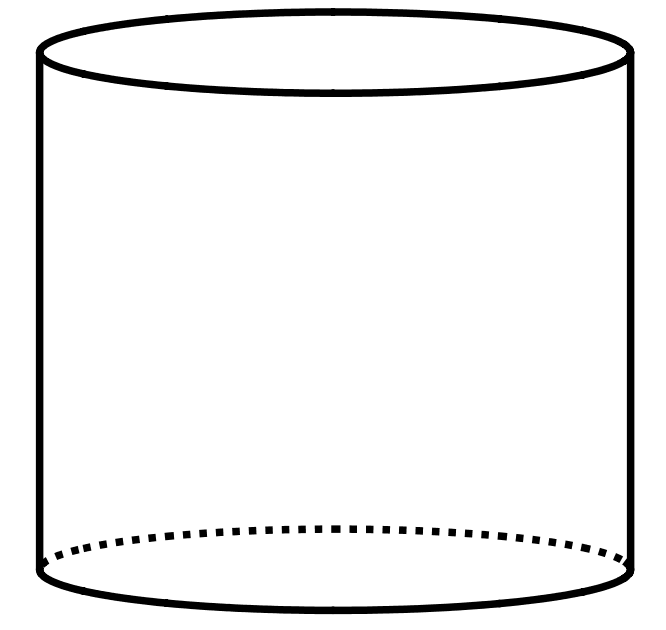
What is the volume of a cone that has the same base area and the same height?
A cone has volume $12\pi$ cubic inches. Its height is 4 inches. What is its radius?
A cone has volume $3 \pi$.
If the cone’s radius is 1, what is its height?
If the cone’s radius is 2, what is its height?
If the cone’s radius is 5, what is its height?
If the cone’s radius is $\frac 1 2$, what is its height?
If the cone's radius in $r$, then what is the height?
Three people are playing near the water. Person A stands on the dock. Person B starts at the top of a pole and ziplines into the water. Person C climbs out of the water and up the zipline pole. Match the people to the graphs where the horizontal axis represents time in seconds and the vertical axis represents height above the water level in feet.
A room is 15 feet tall. An architect wants to include a window that is 6 feet tall. The distance between the floor and the bottom of the window is $b$ feet. The distance between the ceiling and the top of the window is $a$ feet. This relationship can be described by the equation $$a = 15 - (b + 6)$$
A cylinder has a volume of $48 \pi$ cm3 and height $h$. Complete this table for volume of cylinders with the same radius but different heights.
| height (cm) | volume (cm3) | |
|---|---|---|
| row 1 | $h$ | $48\pi$ |
| row 2 | $2h$ | |
| row 3 | $5h$ | |
| row 4 | $\frac h2$ | |
| row 5 | $\frac h5$ |
A cylinder has a radius of 3 cm and a height of 5 cm.
A graduated cylinder that is 24 cm tall can hold 1 L of water. What is the radius of the cylinder? What is the height of the 500 ml mark? The 250 ml mark? Recall that 1 liter (L) is equal to 1000 milliliters (ml).
A 6 oz paper cup is shaped like a cone with a diameter of 4 inches. How many ounces of water will a plastic cylindrical cup with a diameter of 4 inches hold if it is the same height as the paper cup?
Lin’s smart phone was fully charged when she started school at 8:00 a.m. At 9:20 a.m., it was 90% charged, and at noon, it was 72% charged.
When do you think her battery will die?
Is battery life a function of time? If yes, is it a linear function? Explain your reasoning.
There are many cylinders with a height of 18 meters. Let $r$ represent the radius in meters and $V$ represent the volume in cubic meters.
Write an equation that represents the volume $V$ as a function of the radius $r$.
Complete this table, giving three possible examples.
| $r$ | $V$ | |
|---|---|---|
| row 1 | 1 | |
| row 2 | ||
| row 3 |
If the radius of a cylinder is doubled, does the volume double? Explain how you know.
Is the graph of this function a line? Explain how you know.
As part of a competition, Diego must spin around in a circle 6 times and then run to a tree. The time he spends on each spin is represented by $s$ and the time he spends running is $r$. He gets to the tree 21 seconds after he starts spinning.
The table and graph represent two functions. Use the table and graph to answer the questions.
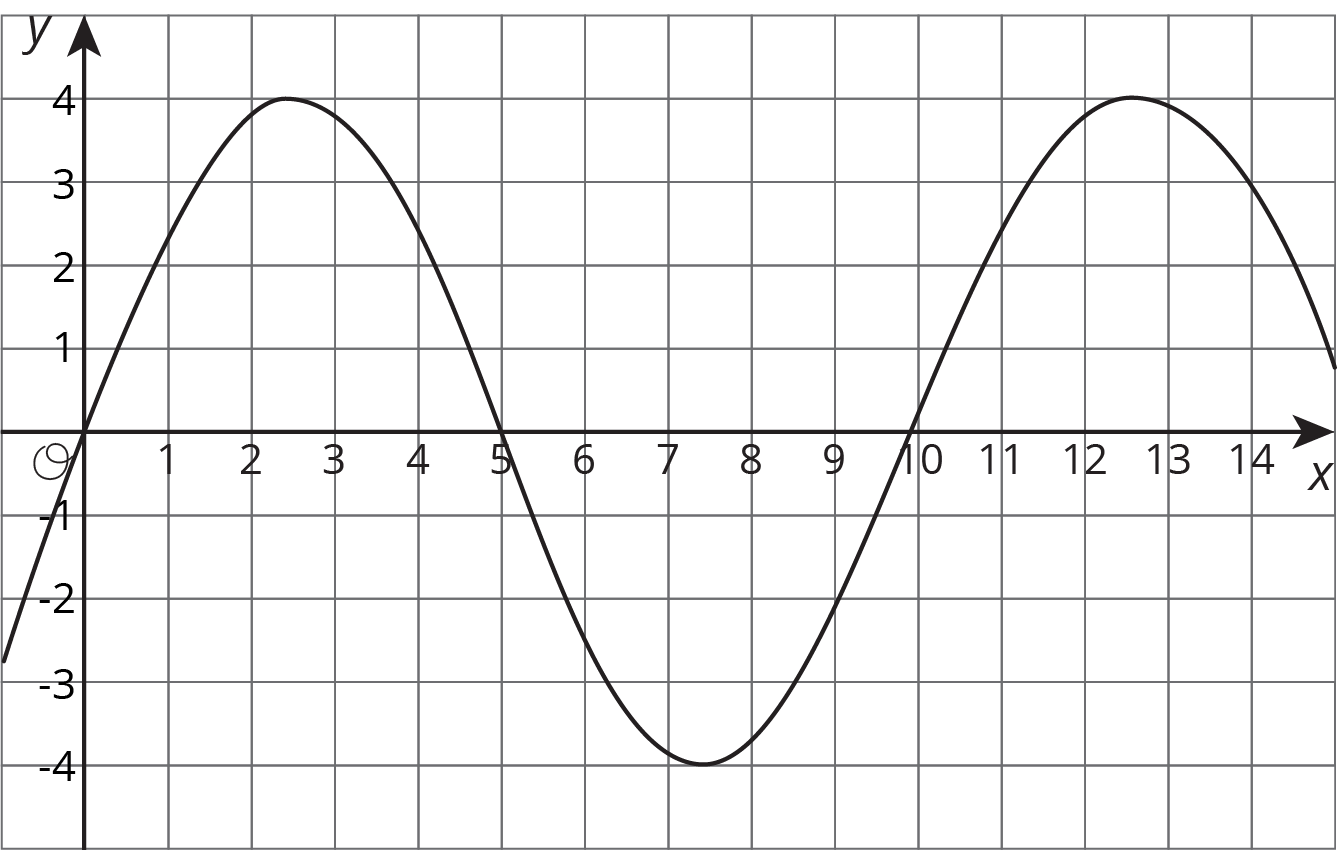
| $x$ | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| $y$ | 3 | -1 | 0 | 4 | 5 | -1 |
A cone has a radius of 3 units and a height of 4 units.
What is this volume of this cone?
Another cone has quadruple the radius, and the same height. How many times larger is the new cone’s volume?
A baseball fits snugly inside a transparent display cube. The length of an edge of the cube is 2.9 inches.
Is the baseball’s volume greater than, less than, or equal to $2.9^3$ cubic inches? Explain how you know.
There are many possible cones with a height of 18 meters. Let $r$ represent the radius in meters and $V$ represent the volume in cubic meters.
Write an equation that represents the volume $V$ as a function of the radius $r$.
Complete this table for the function, giving three possible examples.
| $r$ | $V$ | |
|---|---|---|
| row 1 | 2 | |
| row 2 | ||
| row 3 |
If you double the radius of a cone, does the volume double? Explain how you know.
Is the graph of this function a line? Explain how you know.
A hemisphere fits snugly inside a cylinder with a radius of 6 cm. A cone fits snugly inside the same hemisphere.
Find the hemisphere’s diameter if its radius is 6 cm.
Find the hemisphere’s diameter if its radius is $\frac{1000}{3}$ m.
Find the hemisphere’s diameter if its radius is 9.008 ft.
Find the hemisphere’s radius if its diameter is 6 cm.
Find the hemisphere’s radius if its diameter is $\frac{1000}{3}$ m.
Find the hemisphere’s radius if its diameter is 9.008 ft.
After almost running out of space on her phone, Elena checks with a couple of friends who have the same phone to see how many pictures they have on their phones and how much memory they take up. The results are shown in the table.
| number of photos | 2,523 | 3,148 | 1,875 |
|---|---|---|---|
| memory used in MB | 8,072 | 10,106 | 6,037 |
Match the description of each sphere to its correct volume.
A cube’s volume is 512 cubic units. What is the length of its edge?
If a sphere fits snugly inside this cube, what is its volume?
What fraction of the cube is taken up by the sphere? What percentage is this? Explain or show your reasoning.
Sphere A has radius 2 cm. Sphere B has radius 4 cm.
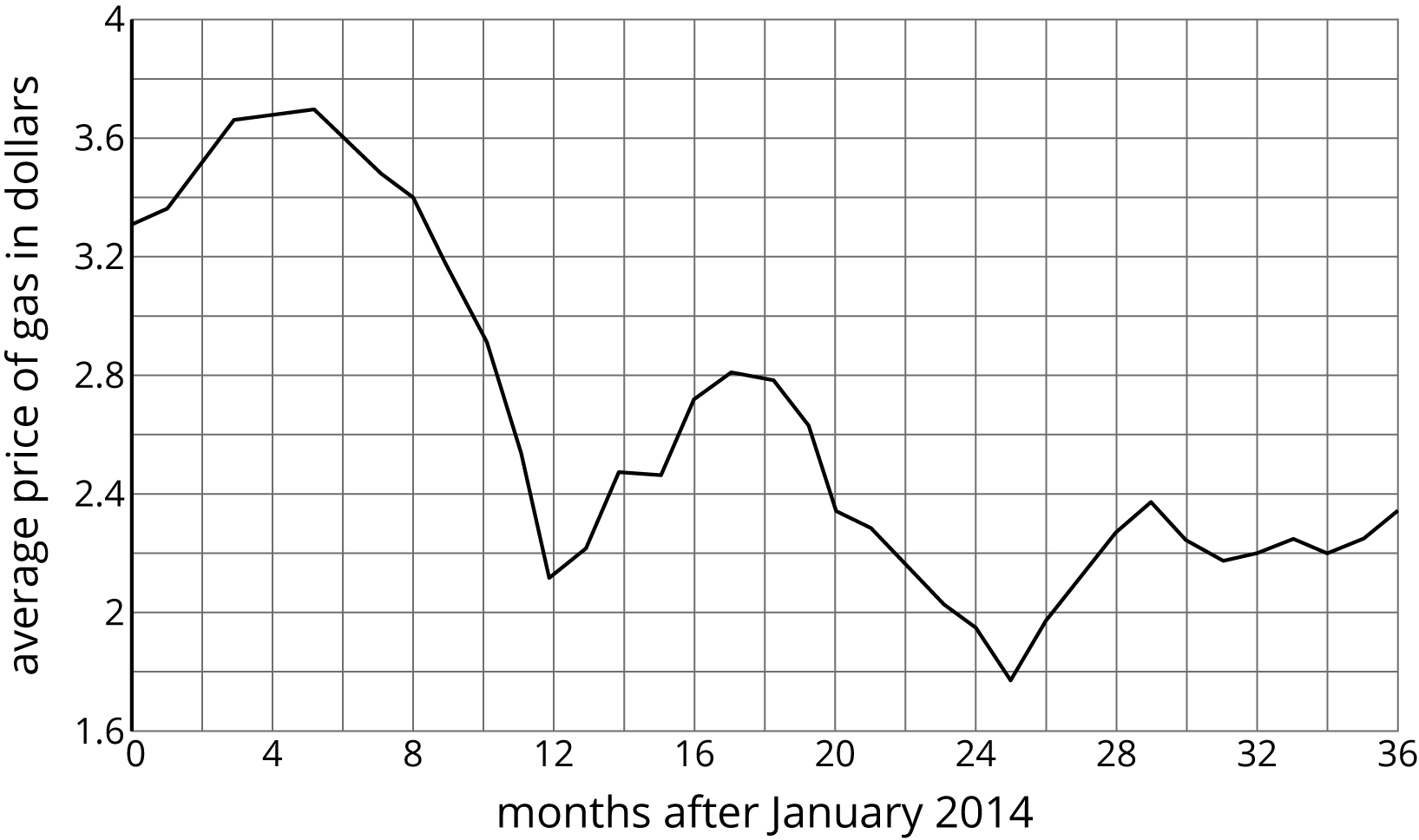
The graph represents the average price of regular gasoline in the United States in dollars as a function of the number of months after January 2014.
While conducting an inventory in their bicycle shop, the owner noticed the number of bicycles is 2 fewer than 10 times the number of tricycles. They also know there are 410 wheels on all the bicycles and tricycles in the store. Write and solve a system of equations to find the number of bicycles in the store.
A scoop of ice cream has a 3 inch radius. How tall should the ice cream cone of the same radius be in order to contain all of the ice cream inside the cone?
Calculate the volume of the following shapes with the given information. For the first three questions, give each answer both in terms of $\pi$ and by using $3.14$ to approximate $\pi$. Make sure to include units.
Sphere with a diameter of 6 inches
Cylinder with a height of 6 inches and a diameter of 6 inches
Cone with a height of 6 inches and a radius of 3 inches
How are these three volumes related?
A coin-operated bouncy ball dispenser has a large glass sphere that holds many spherical balls. The large glass sphere has a radius of 9 inches. Each bouncy ball has radius of 1 inch and sits inside the dispenser.
If there are 243 bouncy balls in the large glass sphere, what proportion of the large glass sphere’s volume is taken up by bouncy balls? Explain how you know.
A farmer has a water tank for cows in the shape of a cylinder with radius of 7 ft and a height of 3 ft. The tank comes equipped with a sensor to alert the farmer to fill it up when the water falls to 20% capacity. What is the volume of the tank be when the sensor turns on?
No practice problems for this lesson.