Lesson 4: Fitting a Line to Data

Let’s look at the scatter plots as a whole.

4.1: Predict This

Here is a scatter plot that shows weights and fuel efficiencies of 20 different types of cars.

If a car weighs 1,750 kg, would you expect its fuel efficiency to be closer to 22 mpg or to 28 mpg? Explain your reasoning.
A scatterplot with 20 data points. The horizontal axis is labeled “weight, in kilograms” and the numbers 1,000 through 2,500, in increments of 250, are indicated. The vertical axis is labeled “fuel efficiency, in miles per gallon” and the numbers 14 through 32, in increments of 2, are indicated. The graph shows the trend of the 20 data points moving linearly downward and to the right. The approximate coordinates of 11 selected data points are as follows: 1,130 comma 28. 1,240 comma 30. 1,400 comma 25. 1,490 comma 23. 1,550 comma 25. 1,590 comma 26. 1,650 comma 19. 1,740 comma 21. 1,775 comma 20. 1,950 comma 19. 2,200 comma 16.

 

4.2: Shine Bright

The prices and sizes of 20 different diamonds are shown in the table and scatter plot.

  weight (carats) actual price (dollars) predicted price (dollars)
row 1 1 3,772 4,429
row 2 1 4,221 4,429
row 3 1 4,032 4,429
row 4 1 5,385 4,429
row 5 1.05 3,942 4,705
row 6 1.05 4,480 4,705
row 7 1.06 4,511 4,760
row 8 1.2 5,544 5,533
row 9 1.3 6,131 6,085
row 10 1.32 5,872 6,195
row 11 1.41 7,122 6,692
row 12 1.5 7,474 7,189
row 13 1.5 5,904 7,189
row 14 1.59 8,706 7,686
row 15 1.61 8,252 7,796
row 16 1.73 9,530 8,459
row 17 1.77 9,374 8,679
row 18 1.85 8,169 9,121
row 19 1.9 9,541 9,397
row 20 2.04 9,125 10,170

The scatter plot shows the prices and weights of the 20 diamonds together with the graph of $y = 5,\!520x- 1,\!091$.

 

The function described by the equation $y = 5,\!520x- 1,\!091$ is a model of the relationship between a diamond’s weight and its price.

This model predicts the price of a diamond from its weight. These predicted prices are shown in the third column of the table.

  1. Two diamonds with a weight of 1.5 carats have different prices. What are their prices? How can you see this in the table? How can you see this in the graph?
  2. The model predicts that when the weight is 1.5 carats, the price will be \$7,189. How can you see this in the graph? How can you see this using the equation?
  3. One of the diamonds weighs 1.9 carats. What does the model predict for its price? How does that compare to the actual price?
  4. Find a diamond where the model makes a very good prediction of the actual price. How can you see this in the table? In the graph?
  5. Find a diamond where the model’s prediction is not very close to the actual price. How can you see this in the table? In the graph?

4.3: The Agony of the Feet

The scatter plot shows widths and lengths of 20 different left feet. Use the double arrows to show or hide the expressions list.

 

  1. Estimate the widths of the longest foot and the shortest foot.

  2. Estimate the lengths of the widest foot and the narrowest foot.

  3. Click on the gray circle next to the words “The Line” in the expressions list. An icon labeled the gray circle. The graph of a linear model should appear. Find the data point that seems weird when compared to the model. What length and width does that point represent?

Summary

Sometimes, we can use a linear function as a model of the relationship between two variables. For example, here is a scatter plot that shows heights and weights of 25 dogs together with the graph of a linear function which is a model for the relationship between a dog’s height and its weight.

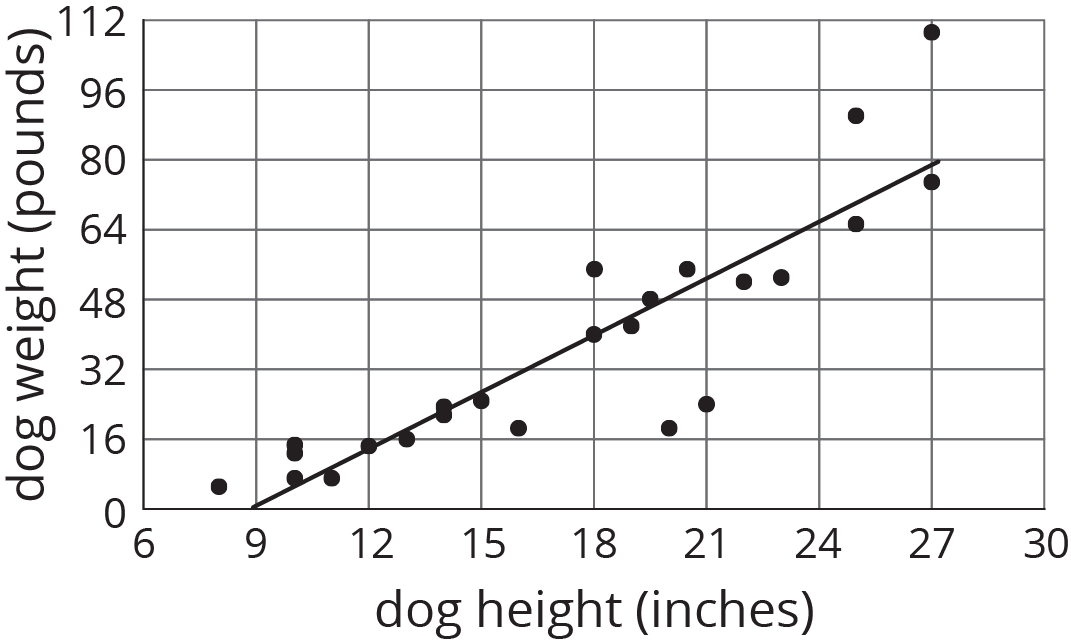
We can see that the model does a good job of predicting the weight given the height for some dogs. These correspond to points on or near the line. The model doesn’t do a very good job of predicting the weight given the height for the dogs whose points are far from the line.

For example, there is a dog that is about 20 inches tall and weighs a little more than 16 pounds. The model predicts that the weight would be about 48 pounds. We say that the model overpredicts the weight of this dog. There is also a dog that is 27 inches tall and weighs about 110 pounds. The model predicts that its weight will be a little less than 80 pounds. We say the model underpredicts the weight of this dog.

Sometimes a data point is far away from the other points or doesn’t fit a trend that all the other points fit. We call these outliers. 

Practice Problems ▶

Glossary

outlier

outlier

In statistics, an outlier is a data value that is way outside the group of other values.