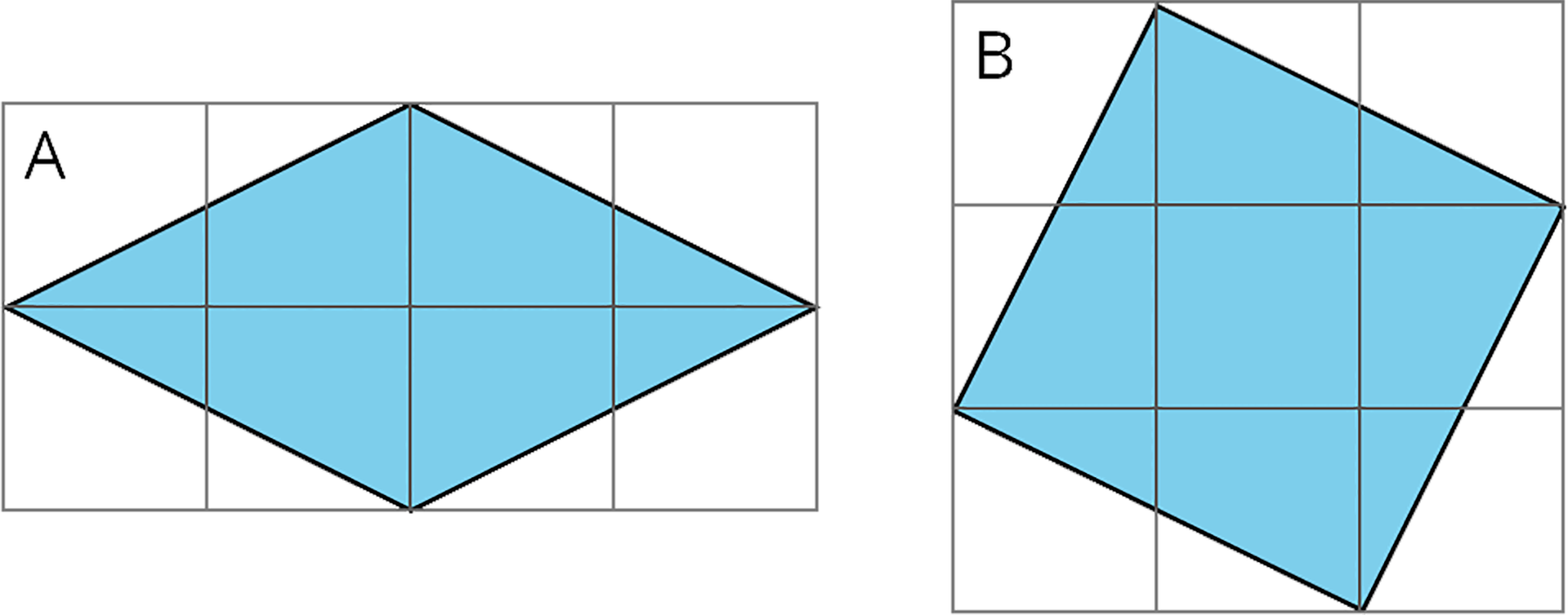
1.1: Two Regions
Which shaded region is larger? Explain your reasoning.
Let’s investigate the squares and their side lengths.
Which shaded region is larger? Explain your reasoning.

Find the area of each shaded square (in square units).



Any triangle with a base of 13 and a height of 5 has an area of $\frac{65}{2}$.
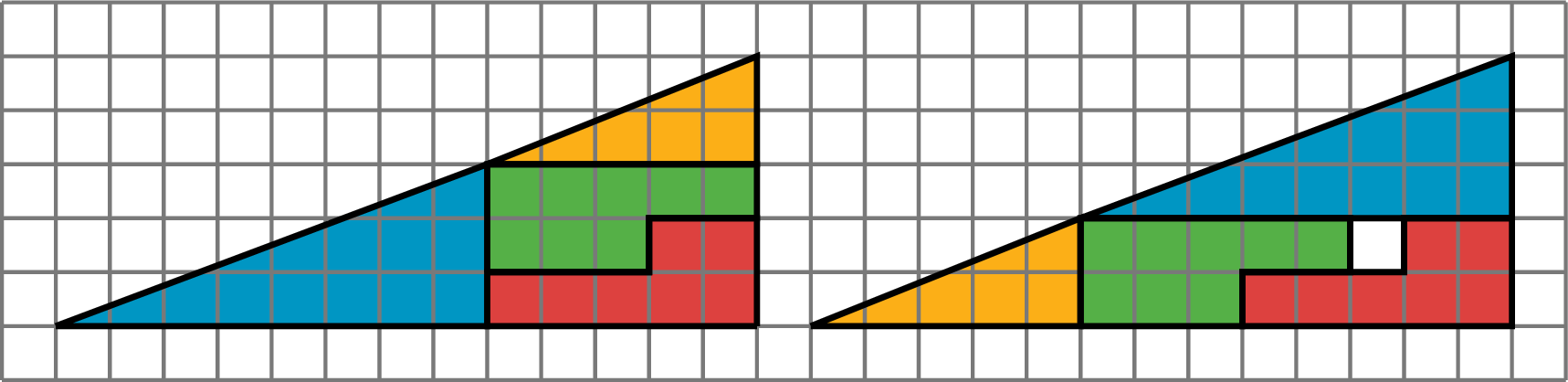
Both shapes in the figure have been partitioned into the same four pieces. Find the area of each of the piece and verify the corresponding parts are the same in each picture. There appears to be one extra unit of area in the right figure than in the left one. If all of the pieces have the same area, how is this possible?

Find the areas of squares D, E, and F. Which of these squares must have a side length that is greater than 5 but less than 6? Explain how you know.

Use the applet to determine the total area of the five shapes, $D$, $E$, $F$, $G$, and $H$. Assume each small square is equal to 1 square unit.
The area of a square with side length 12 units is $12^2$ or 144 units2.
The side length of a square with area 900 units2 is 30 units because $30^2 = 900$.
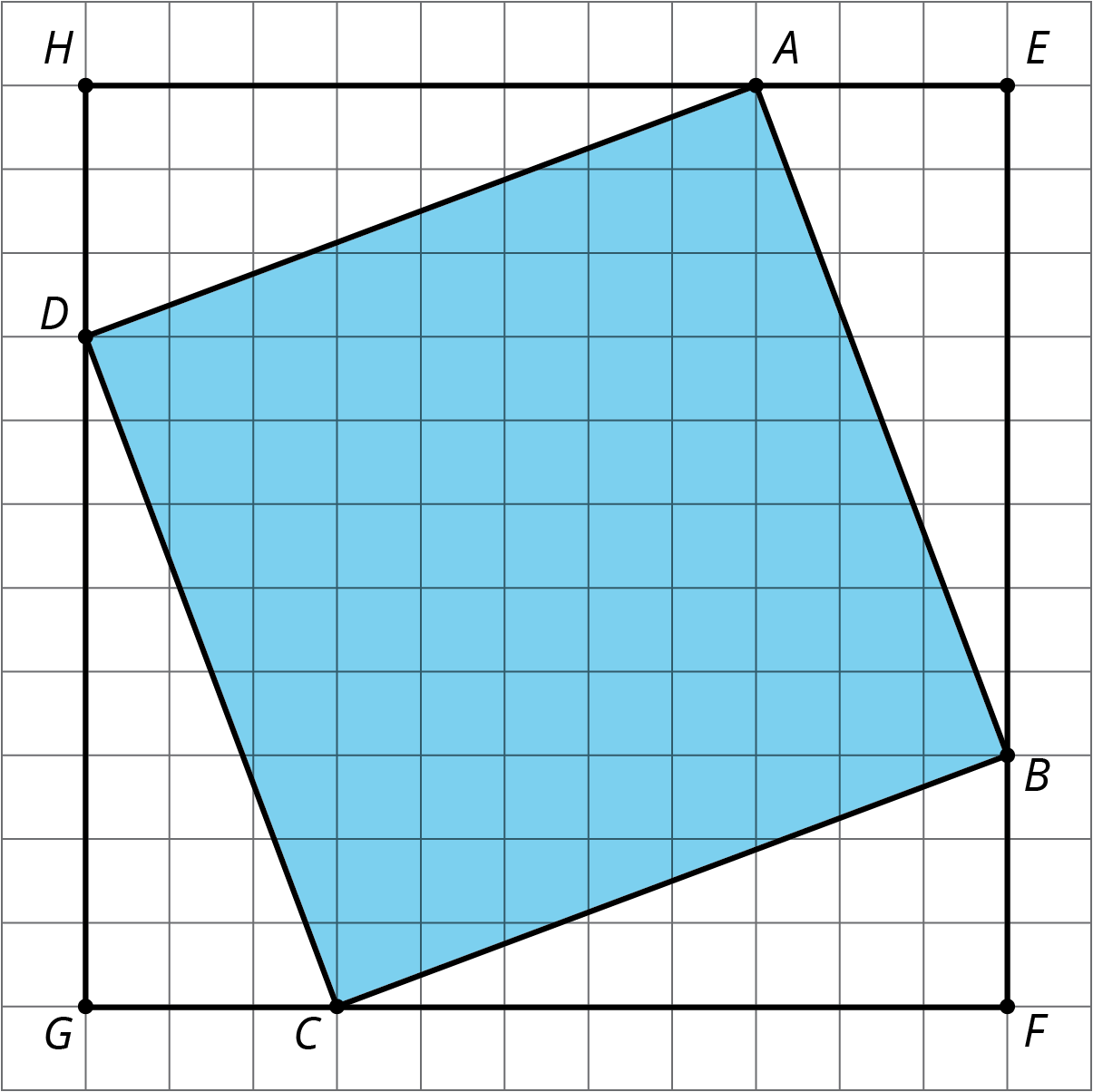
Sometimes we want to find the area of a square but we don’t know the side length. For example, how can we find the area of square $ABCD$?
One way is to enclose it in a square whose side lengths we do know.

The outside square $EFGH$ has side lengths of 11 units, so its area is 121 units2. The area of each of the four triangles is $\frac12 \boldcdot 8 \boldcdot 3 = 12$, so the area of all four together is $4 \boldcdot 12 = 48$ units2. To get the area of the shaded square, we can take the area of the outside square and subtract the areas of the 4 triangles. So the area of the shaded square $ABCD$ is $121 - 48 = 73$ or 73 units2.