Let’s explore some applications of the Pythagorean Theorem.
Which estimate is closest to the actual value of the expression? Explain your reasoning.
$\sqrt{24}$
4
4.5
5
$\sqrt7$
2
2.5
3
$\sqrt{42}$
6
6.5
7
$\sqrt{10}$ + $\sqrt{97}$
13
13.25
13.5
Mai and Tyler were standing at one corner of a large rectangular field and decided to race to the opposite corner. Since Mai had a bike and Tyler did not, they thought it would be a fairer race if Mai rode along the sidewalk that surrounds the field while Tyler ran the shorter distance directly across the field. The field is 100 meters long and 80 meters wide. Tyler can run at around 5 meters per second, and Mai can ride her bike at around 7.5 meters per second.
Before making any calculations, who do you think will win? By how much? Explain your thinking.
A calculator may be necessary to answer the following questions. Round answers to the nearest hundredth.
If you could give the loser of the race a head start, how much time would they need in order for both people to arrive at the same time?
If you could make the winner go slower, how slow would they need to go in order for both people to arrive at the same time?
Here are two rectangular prisms:
The Pythagorean Theorem can be used to solve any problem that can be modeled with a right triangle where the lengths of two sides are known and the length of the other side needs to be found. For example, let’s say a cable is being placed on level ground to support a tower. It’s a 17-foot cable, and the cable should be connected 15 feet up the tower. How far away from the bottom of the tower should the other end of the cable connect to the ground?
It is often very helpful to draw a diagram of a situation, such as the one shown here:
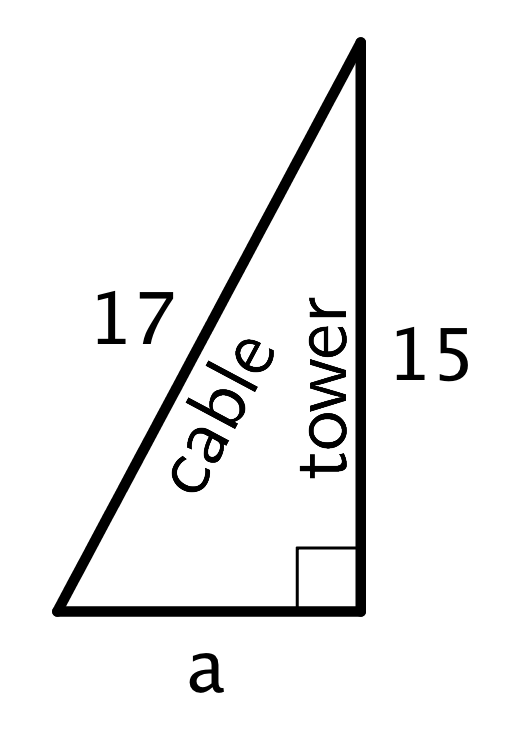
It’s assumed that the tower makes a right angle with the ground. Since this is a right triangle, the relationship between its sides is $a^2+b^2=c^2$, where $c$ represents the length of the hypotenuse and $a$ and $b$ represent the lengths of the other two sides. The hypotenuse is the side opposite the right angle. Making substitutions gives $a^2+15^2=17^2$. Solving this for $a$ gives $a=8$. So, the other end of the cable should connect to the ground 8 feet away from the bottom of the tower.
