Lesson 11: Finding Distances in the Coordinate Plane

Let’s find distances in the coordinate plane.

11.1: Closest Distance

  1. Order the following pairs of coordinates from closest to farthest apart. Be prepared to explain your reasoning.

    1. $(2,4)$ and $(2,10)$

    2. $(\text -3,6)$ and $(5,6)$

    3. $(\text -12, \text -12)$ and $(\text -12, \text -1)$

    4. $(7, 0)$ and $(7,\text -9)$

    5. $(1, \text -10)$ and $(\text -4,\text -10)$

  2. Name another pair of coordinates that would be closer together than the first pair on your list.

  3. Name another pair of coordinates that would be farther apart than the last pair on your list.

11.2: How Far Apart?

Find the distances between the three points shown.

11.3: Perimeters with Pythagoras

Two triangles labeled “J” and “K” are graphed in the coordinate plane with the origin labeled “O”. The numbers negative 3 through 10 are indicated on the horizontal axis and the numbers negative 5 through 4 are indicated on the vertical axis. The triangles have the following vertices: Triangle “J”: Negative 2 comma negative 2. 2 comma negative 4. 4 comma 2. Triangle “K”: 7 comma 4. 9 comma 2. 8 comma negative 5.

  1. Which figure do you think has the longer perimeter?
  2. Select one figure and calculate its perimeter. Your partner will calculate the perimeter of the other. Were you correct about which figure had the longer perimeter?

11.4: Finding the Right Distance

Have each person in your group select one of the sets of coordinate pairs shown here. Then calculate the length of the line segment between those two coordinates. Once the values are calculated, have each person in the group briefly share how they did their calculations.

  • $(\text -3,1)$ and $(5,7)$

  • $(\text -1,\text -6)$ and $(5,2)$

  • $(\text -1,2)$ and $(5,\text -6)$

  • $(\text -2,\text -5)$ and $(6,1)$

  1. How does the value you found compare to the rest of your group?
  2. In your own words, write an explanation to another student for how to find the distance between any two coordinate pairs.

Summary

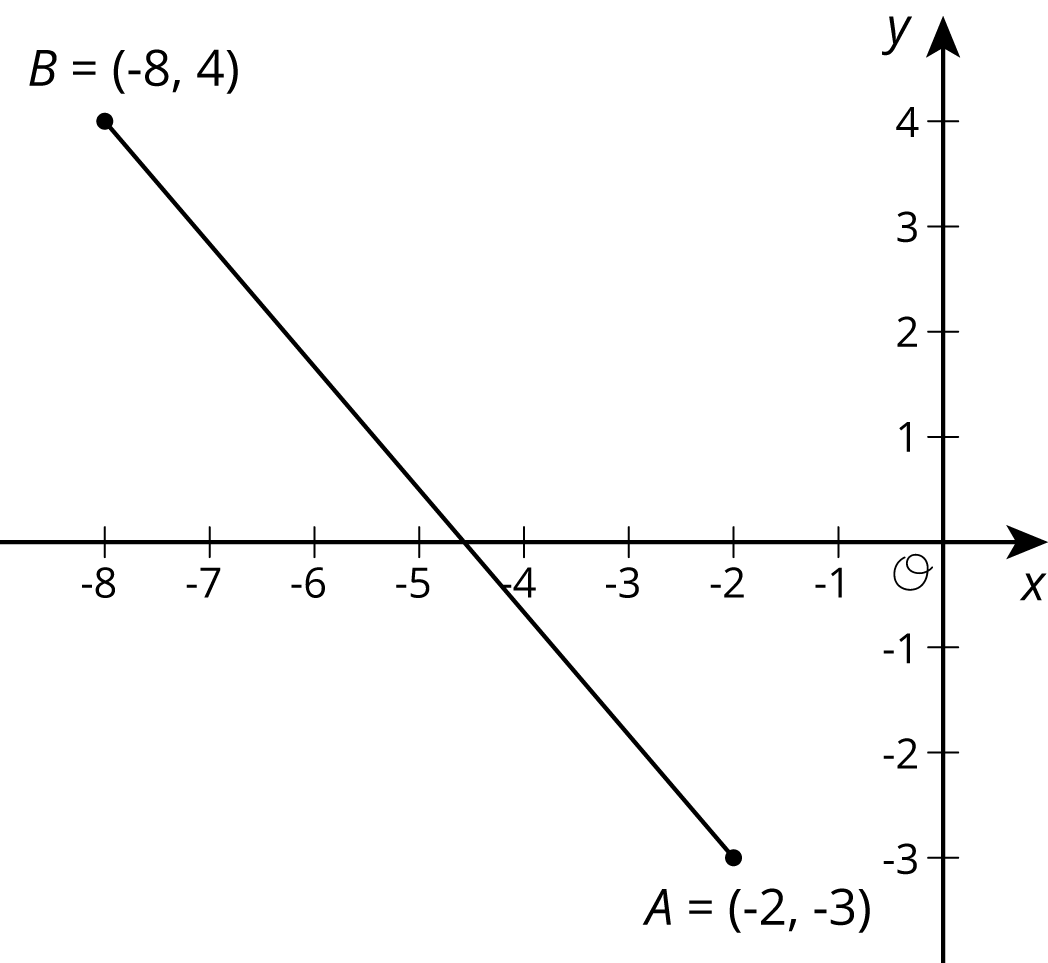
We can use the Pythagorean Theorem to find the distance between any two points on the coordinate plane. For example, if the coordinates of point $A$ are $(\text-2,\text-3)$, and the coordinates of point $B$ are $(\text-8,4)$, let’s find the distance between them. This distance is also the length of line segment $AB$. It is a good idea to plot the points first.

The graph of a line segment in the coordinate plane with the origin labeled “O”. On the x-axis, the numbers negative 8 through 0 are indicated. On the y-axis, the numbers negative 3 through 4 are indicated. The line segment begins to the left of the y axis and above the x axis at the point labeled B where point B has coordinates negative 8 comma 4. The line segment slants downward and to the right, crosses the x axis and ends at the point labeled A. Point A has coordinates negative 2 comma negative 3.

Think of the distance between $A$ and $B$, or the length of segment $AB$, as the hypotenuse of a right triangle. The lengths of the legs can be deduced from the coordinates of the points.

A triangle is graphed in the coordinate plane with the origin labeled “O”. On the x-axis, the numbers negative 8 through negative one are indicated. On the y-axis, the numbers negative 3 through 4 are indicated. Two of the vertices, point A and point B, of the triangle are labeled. Point A is located at negative 2 comme negative 3 and point B is located at negative 8 comma 4. A vertical line is drawn from Point B directly down and a horizontal line is drawn from Point A to the left until the two lines meet creating the third vertex of the triangle. The two lines meet at the point with coordinates negative 8 comma negative 3. The vertical line is labeled with the text "the absolute value of four minus negative three equals 7". The horizontal line is labeled with the text "the absolute value of -8 minus -2 equals 6."

The length of the horizontal leg is 6, which can be seen in the diagram, but it is also the distance between the $x$-coordinates of $A$ and $B$ since $|\text-8-\text-2|=6$. The length of the vertical leg is 7, which can be seen in the diagram, but this is also the distance between the $y$-coordinates of $A$ and $B$ since $|4 - \text-3|=7$.

 

Once the lengths of the legs are known, we use the Pythagorean Theorem to find the length of the hypotenuse, $AB$, which we can represent with $c$. Since $c$ is a positive number, there is only one value it can take:

\(\begin{align} 6^2+7^2&=c^2 \\ 36+49&=c^2 \\ 85&=c^2 \\ \sqrt{85}&=c \\ \end{align}\)

This length is a little longer than 9, since 85 is a little longer than 81. Using a calculator gives a more precise answer, $\sqrt{85} \approx 9.22$.

Practice Problems ▶