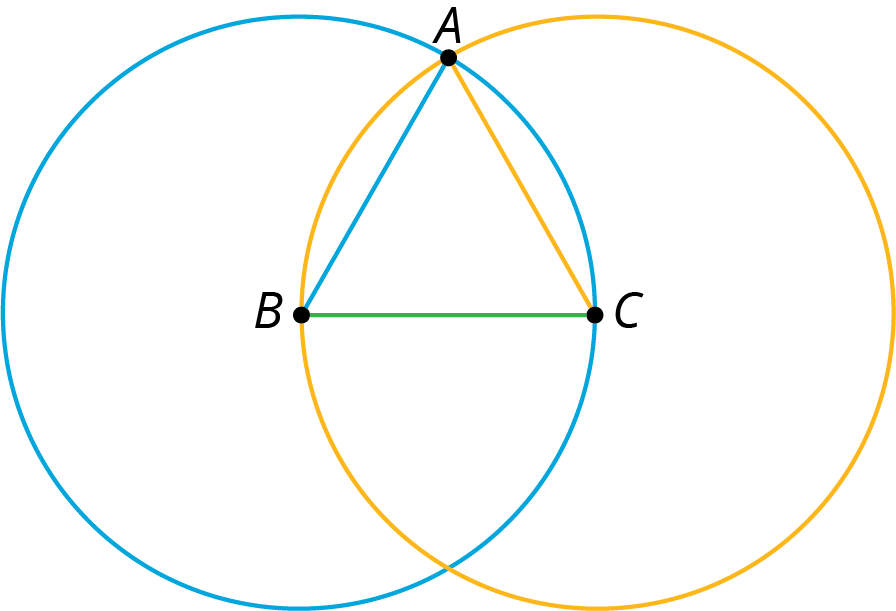
2.1: Notice and Wonder: Intersecting Circles
What do you notice? What do you wonder?
Let’s investigate some more squares.
What do you notice? What do you wonder?

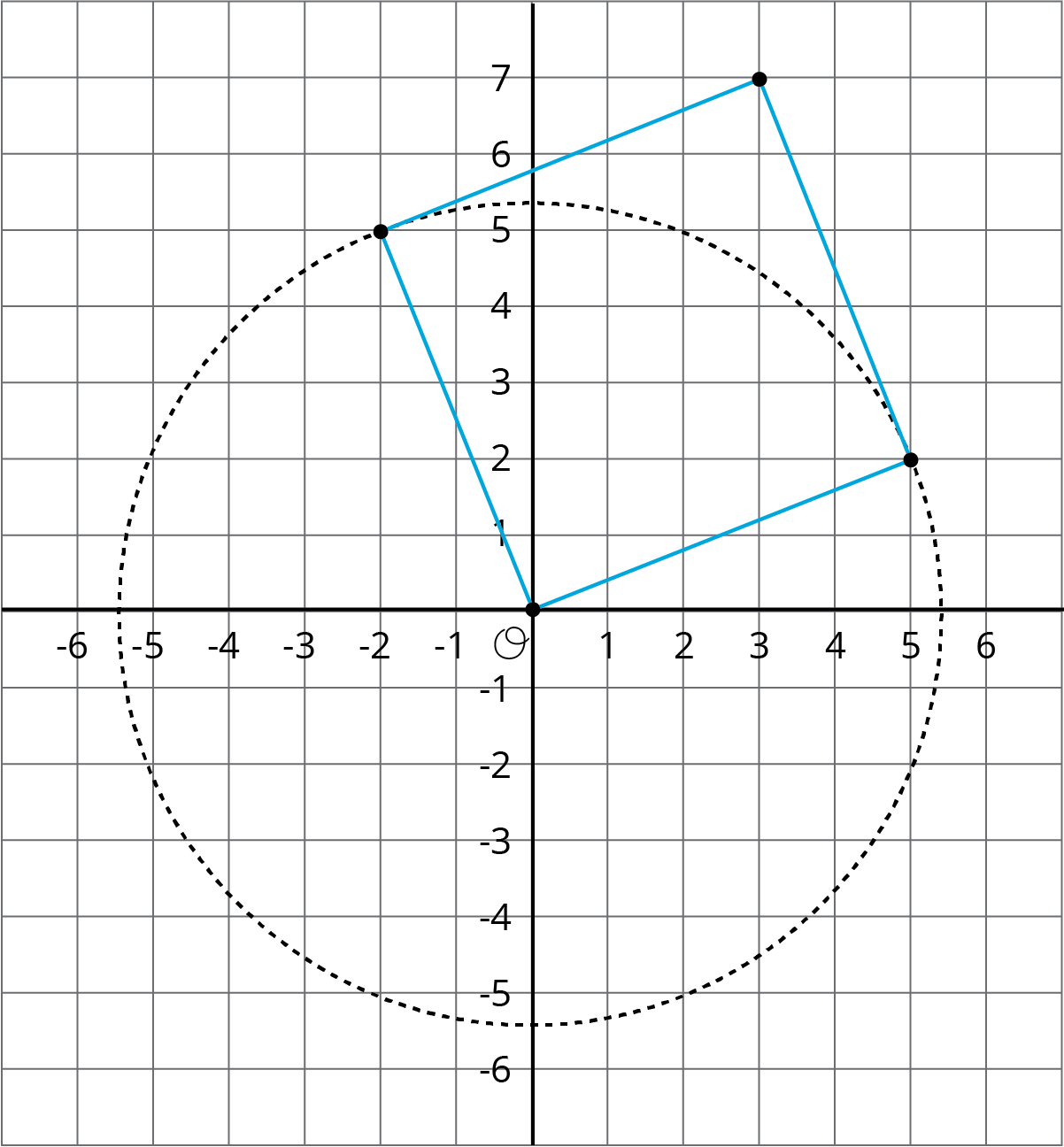
Use the circle to estimate the area of the square shown here:

Use the grid to check your answer to the first problem.
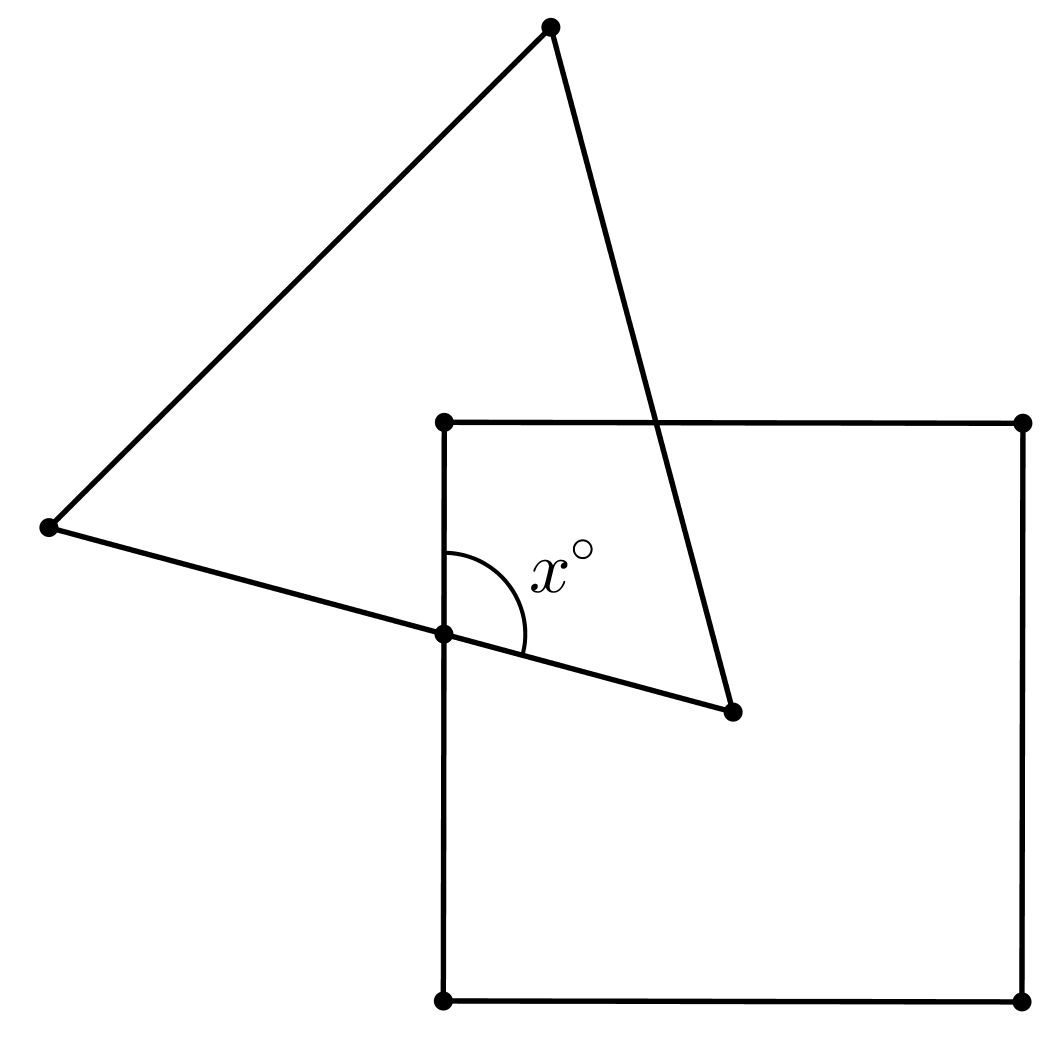
One vertex of the equilateral triangle is in the center of the square, and one vertex of the square is in the center of the equilateral triangle. What is $x$?
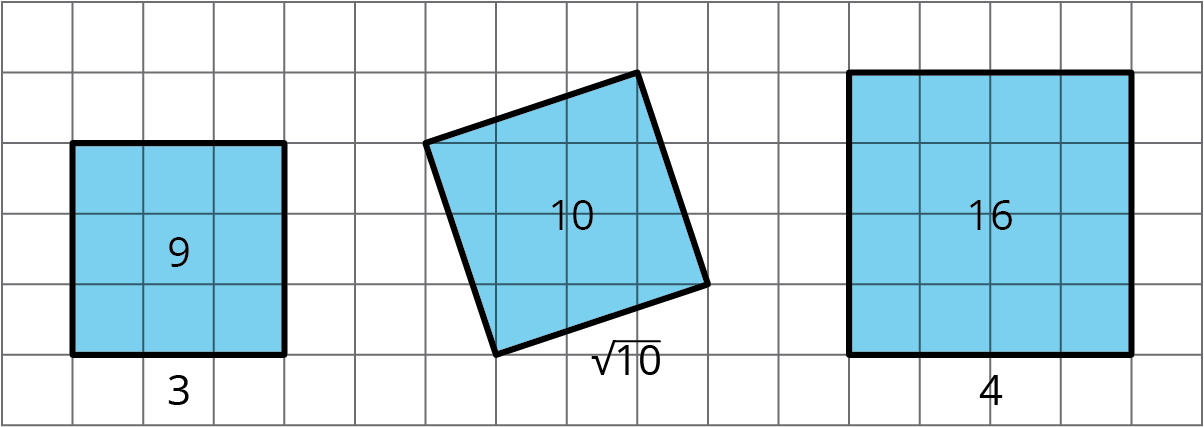
Find the area of each square and estimate the side lengths using your geometry toolkit. Then write the exact lengths for the sides of each square.

| side length, $s$ | 0.5 | 1.5 | 2.5 | 3.5 | |||||
|---|---|---|---|---|---|---|---|---|---|
| row 1 | area, $a$ | 1 | 4 | 9 | 16 |
| side length, $s$ | 4.5 | 5.5 | 6.5 | 7.5 | |||||
|---|---|---|---|---|---|---|---|---|---|
| row 1 | area, $a$ | 25 | 36 | 49 | 64 |
Plot the points, $(s, a)$, on the coordinate plane shown here.
Use this graph to estimate the side lengths of the squares in the first question. How do your estimates from the graph compare to the estimates you made initially using your geometry toolkit?
We saw earlier that the area of square ABCD is 73 units2.

What is the side length? The area is between $8^2 = 64$ and $9^2 = 81$, so the side length must be between 8 units and 9 units. We can also use tracing paper to trace a side length and compare it to the grid, which also shows the side length is between 8 units and 9 units. But we want to be able to talk about its exact length. In order to write “the side length of a square whose area is 73 square units,” we use the square root symbol. “The square root of 73” is written $\sqrt{73}$, and it means “the length of a side of a square whose area is 73 square units.”
We say the side length of a square with area 73 units2 is $\sqrt{73}$ units. This means that
All of these statements are also true:
$\sqrt{9}=3$ because $3^2=9$
$\sqrt{16}=4$ because $4^2=16$
$\sqrt{10}$ units is the side length of a square whose area is 10 units2, and $\left(\sqrt{10}\right)^2=10$
The square root of a positive number $x$, written $\sqrt{x}$, is the positive number whose square is $x$. For example, $\sqrt{4} = 2$ because $2^2 = 4$ and $2$ is positive. The square root of 0 is 0.