5.1: True or False: Squared
Decide if each statement is true or false.
$\left( \sqrt{5} \right)^2=5$
$\left(\sqrt{9}\right)^2 = 3$
$7 = \left(\sqrt{7}\right)^2$
$\left(\sqrt{10}\right)^2 = 100$
$\left(\sqrt{16}\right)= 2^2$
Let’s approximate square roots.
Decide if each statement is true or false.
$\left( \sqrt{5} \right)^2=5$
$\left(\sqrt{9}\right)^2 = 3$
$7 = \left(\sqrt{7}\right)^2$
$\left(\sqrt{10}\right)^2 = 100$
$\left(\sqrt{16}\right)= 2^2$
What two whole numbers does each square root lie between? Be prepared to explain your reasoning.
The numbers $x$, $y$, and $z$ are positive, and $x^2 = 3$, $y^2 = 16$, and $z^2 = 30$.
In general, we can approximate the values of square roots by observing the whole numbers around it, and remembering the relationship between square roots and squares. Here are some examples:
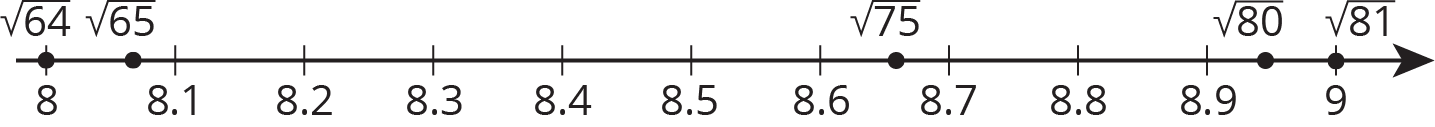
If we want to find a square root between two whole numbers, we can work in the other direction. For example, since $22^2 = 484$ and $23^2 = 529$, then we know that $\sqrt{500}$ (to pick one possibility) is between 22 and 23.
Many calculators have a square root command, which makes it simple to find an approximate value of a square root.