8.1: Which One Doesn’t Belong: Equations
Which one doesn’t belong?
$3^2 + b^2 = 5^2$
$b^2 = 5^2 - 3^2 $
$3^2 + 5^2 = b^2$
Let’s find missing side lengths of right triangles.
Which one doesn’t belong?
$3^2 + b^2 = 5^2$
$b^2 = 5^2 - 3^2 $
$3^2 + 5^2 = b^2$
Label all the hypotenuses with $c$.


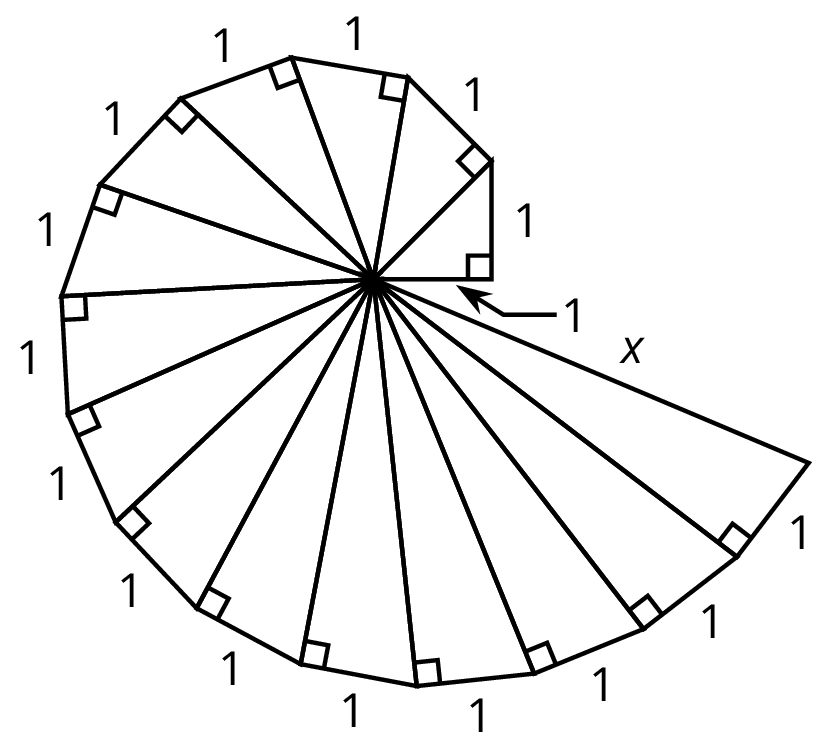
The spiral in the figure is made by starting with a right triangle with both legs measuring one unit each. Then a second right triangle is built with one leg measuring one unit, and the other leg being the hypotenuse of the first triangle. A third right triangle is built on the second triangle’s hypotenuse, again with the other leg measuring one unit, and so on.
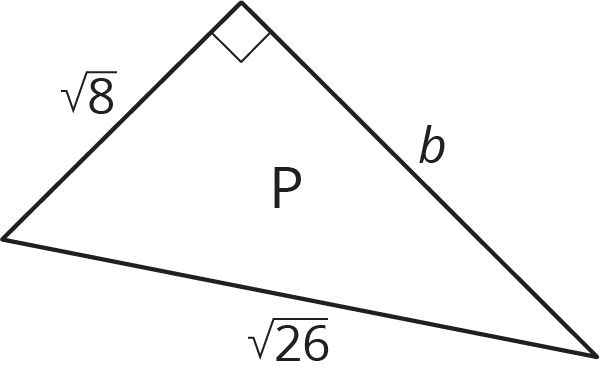
There are many examples where the lengths of two legs of a right triangle are known and can be used to find the length of the hypotenuse with the Pythagorean Theorem. The Pythagorean Theorem can also be used if the length of the hypotenuse and one leg is known, and we want to find the length of the other leg. Here is a right triangle, where one leg has a length of 5 units, the hypotenuse has a length of 10 units, and the length of the other leg is represented by $g$.
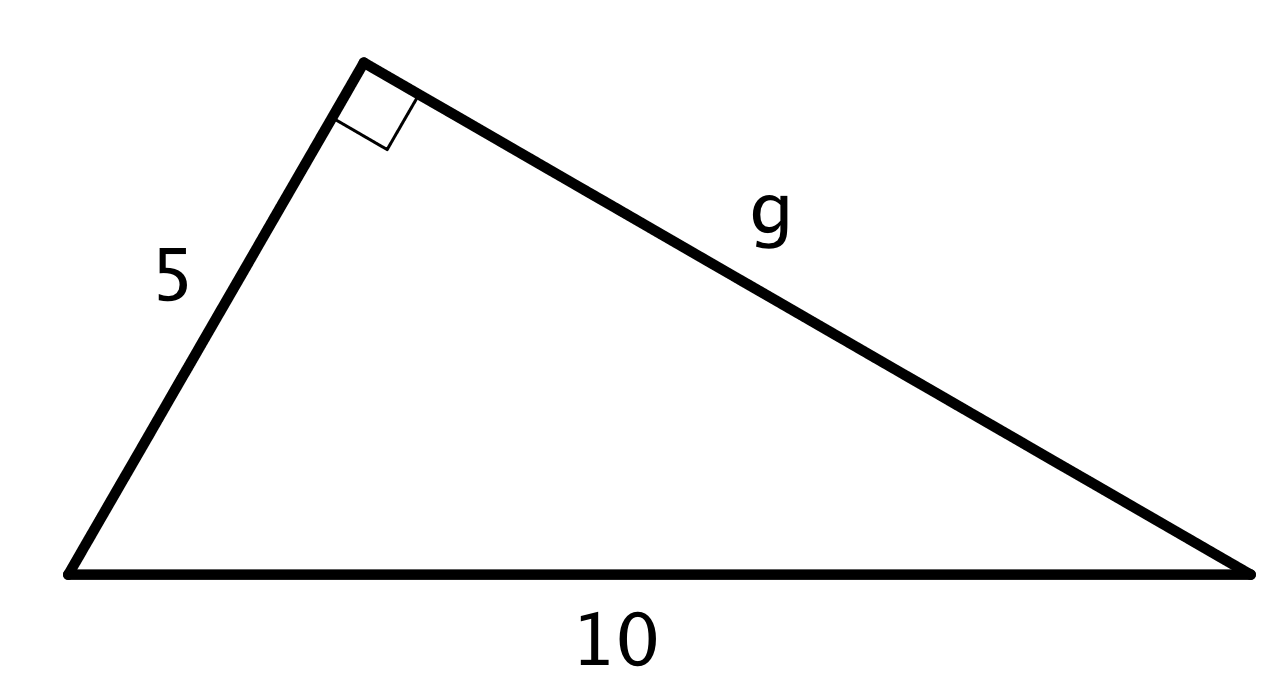
Start with $a^2+b^2=c^2$, make substitutions, and solve for the unknown value. Remember that $c$ represents the hypotenuse: the side opposite the right angle. For this triangle, the hypotenuse is 10.
\(\begin{align} a^2+b^2&=c^2 \\ 5^2+g^2&=10^2 \\ g^2&=10^2-5^2 \\ g^2&=100-25 \\ g^2&=75 \\ g&=\sqrt{75} \\ \end{align}\)
Use estimation strategies to know that the length of the other leg is between 8 and 9 units, since 75 is between 64 and 81. A calculator with a square root function gives $\sqrt{75} \approx 8.66$.