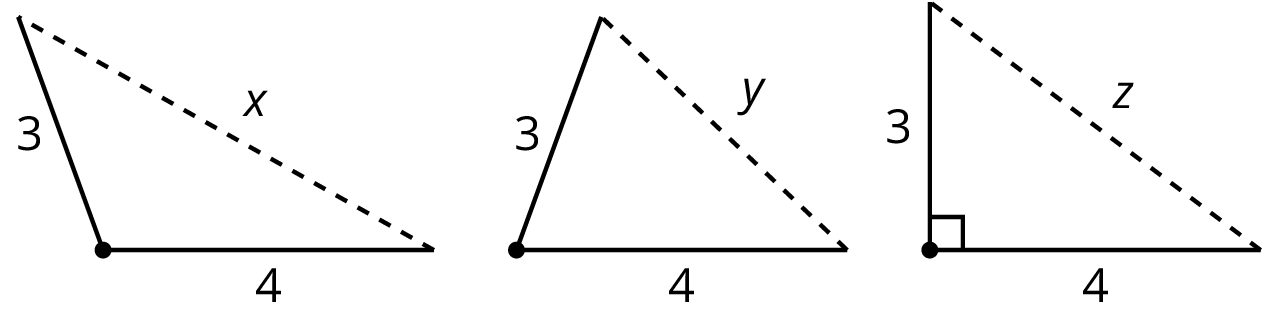
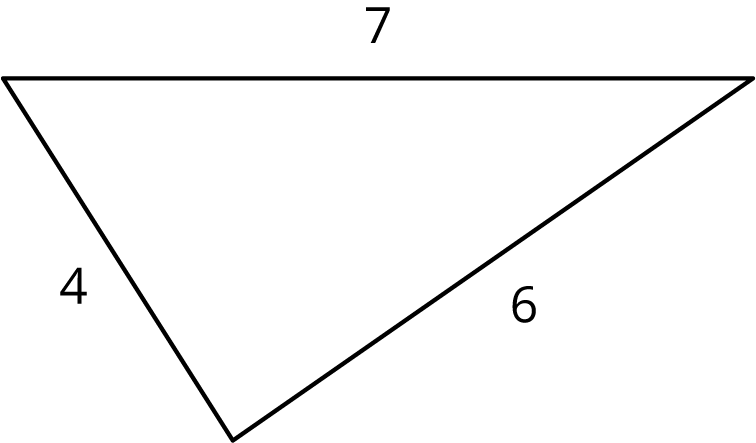
What if it isn’t clear whether a triangle is a right triangle or not? Here is a triangle:
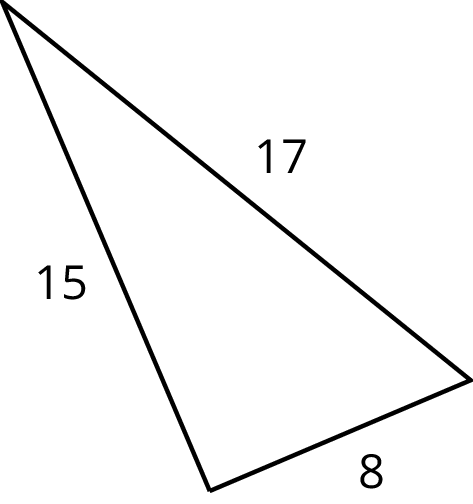
Is it a right triangle? It’s hard to tell just by looking, and it may be that the sides aren’t drawn to scale.
If we have a triangle with side lengths $a$, $b$, and $c$, with $c$ being the longest of the three, then the converse of the Pythagorean Theorem tells us that any time we have $a^2+b^2=c^2$, we must have a right triangle. Since $8^2+15^2=64+225=289=17^2$, any triangle with side lengths 8, 15, and 17 must be a right triangle.
Together, the Pythagorean Theorem and its converse provide a one-step test for checking to see if a triangle is a right triangle just using its side lengths. If $a^2+b^2=c^2$, it is a right triangle. If $a^2+b^2\neq c^2$, it is not a right triangle.