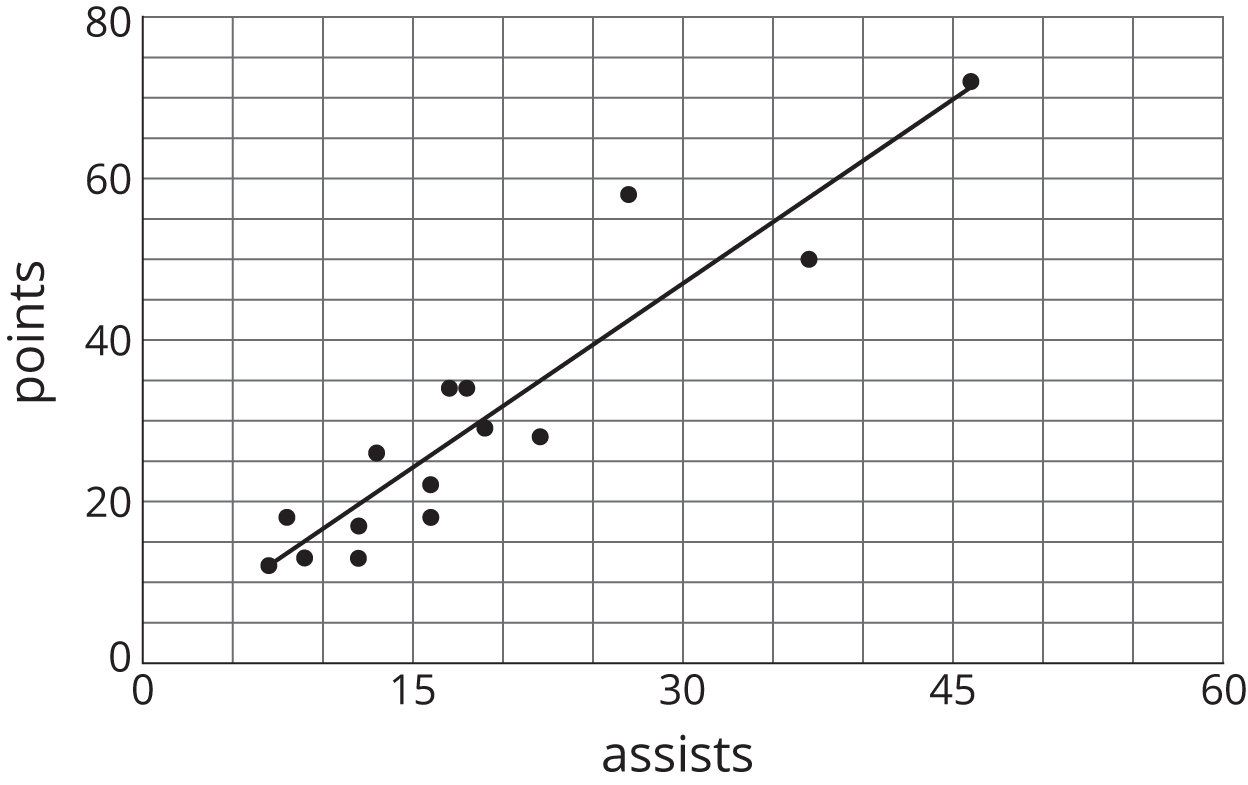
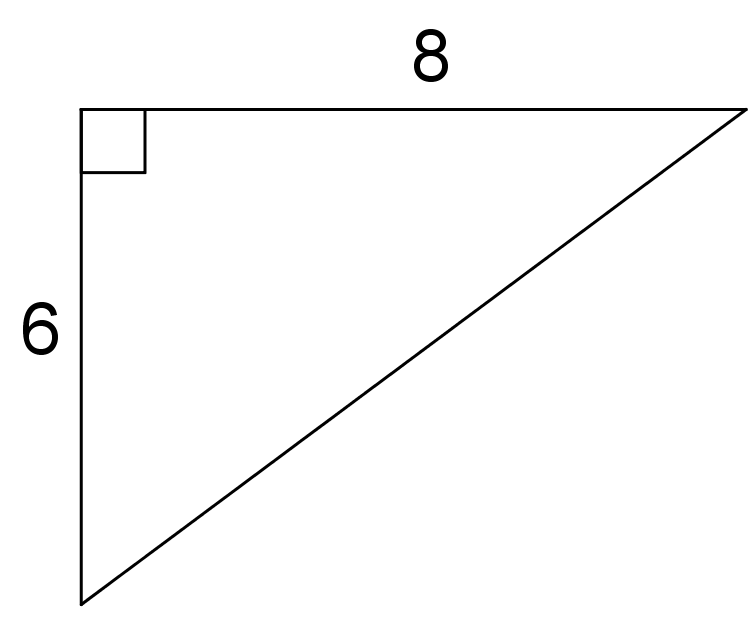
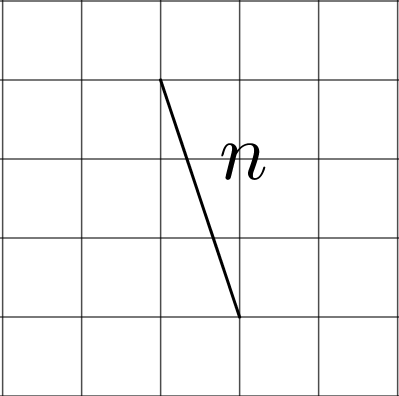
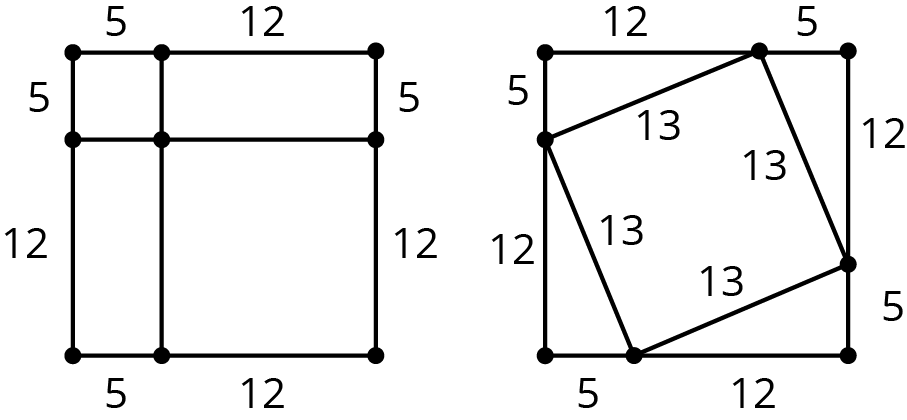
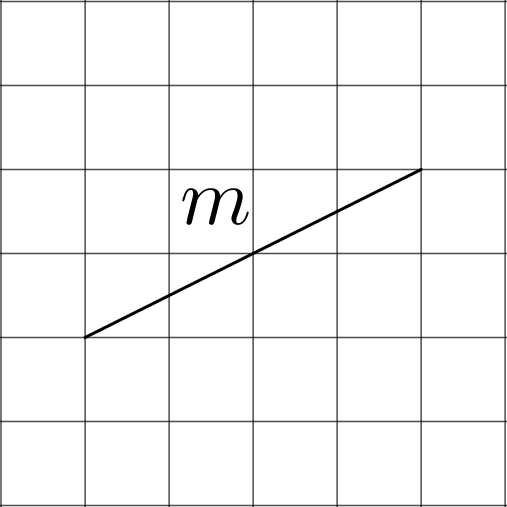
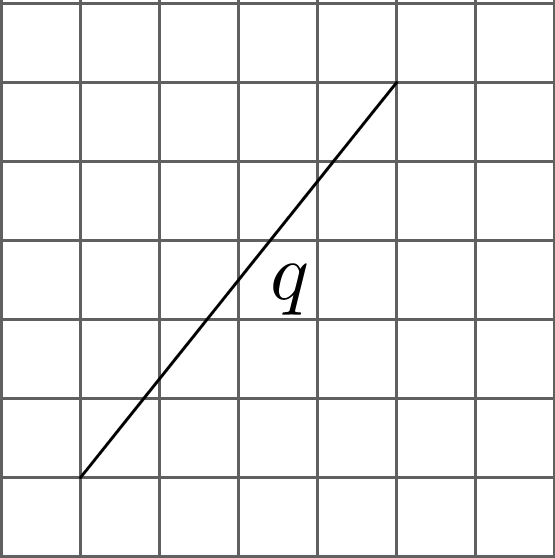
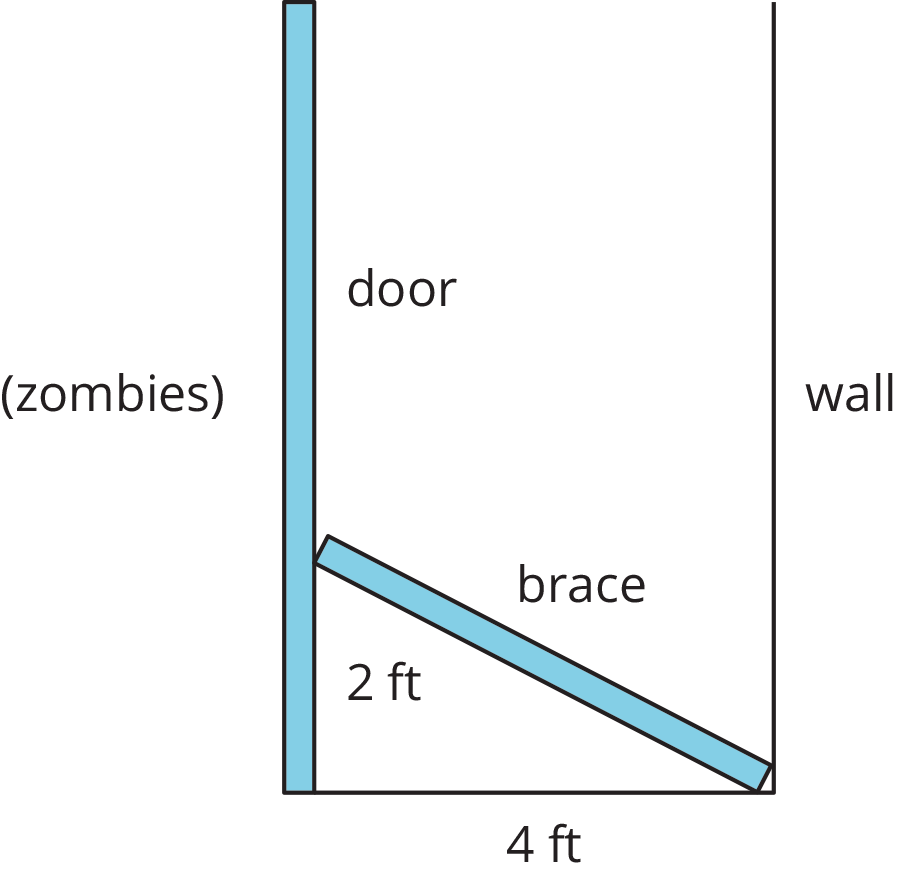
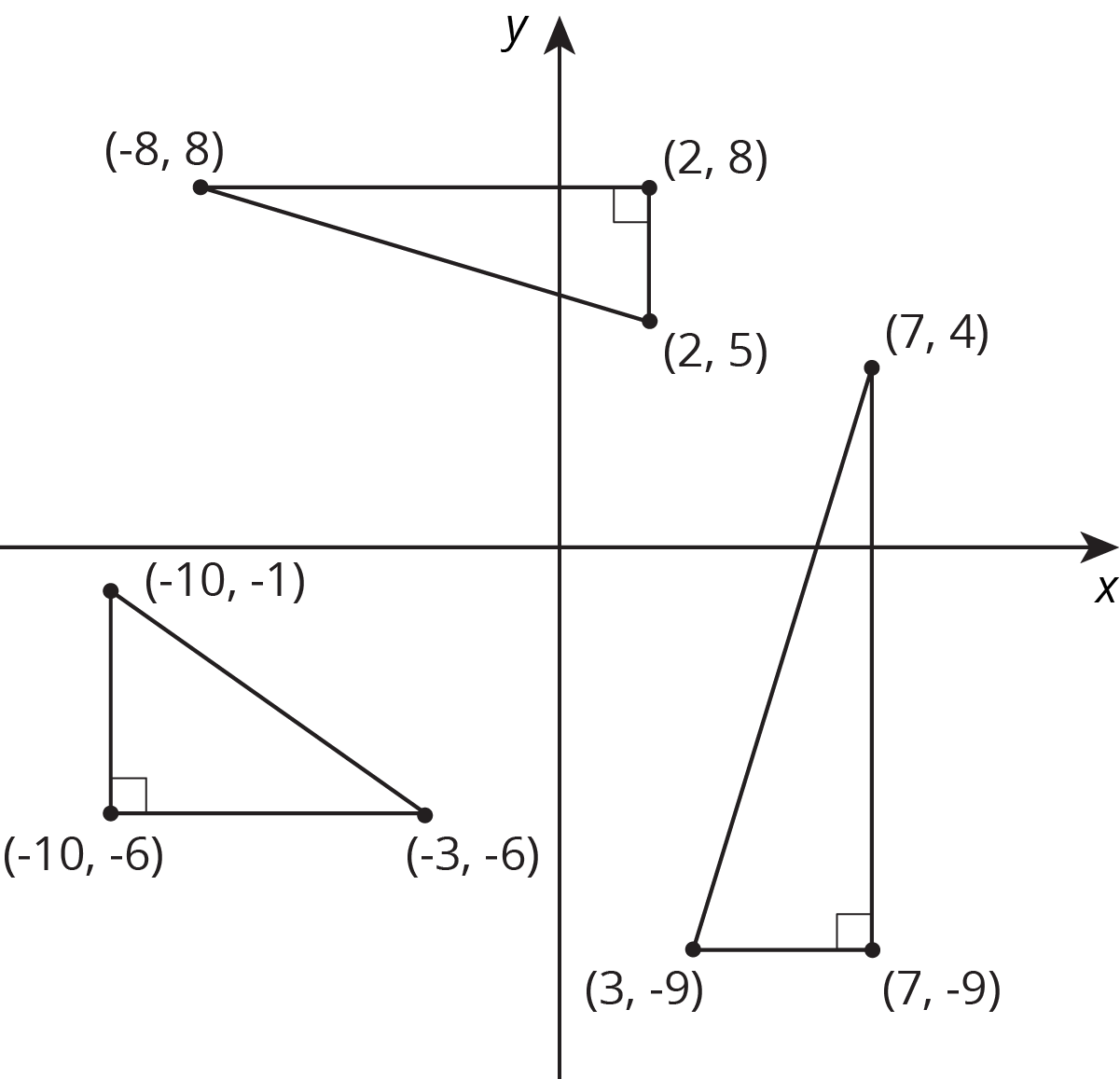
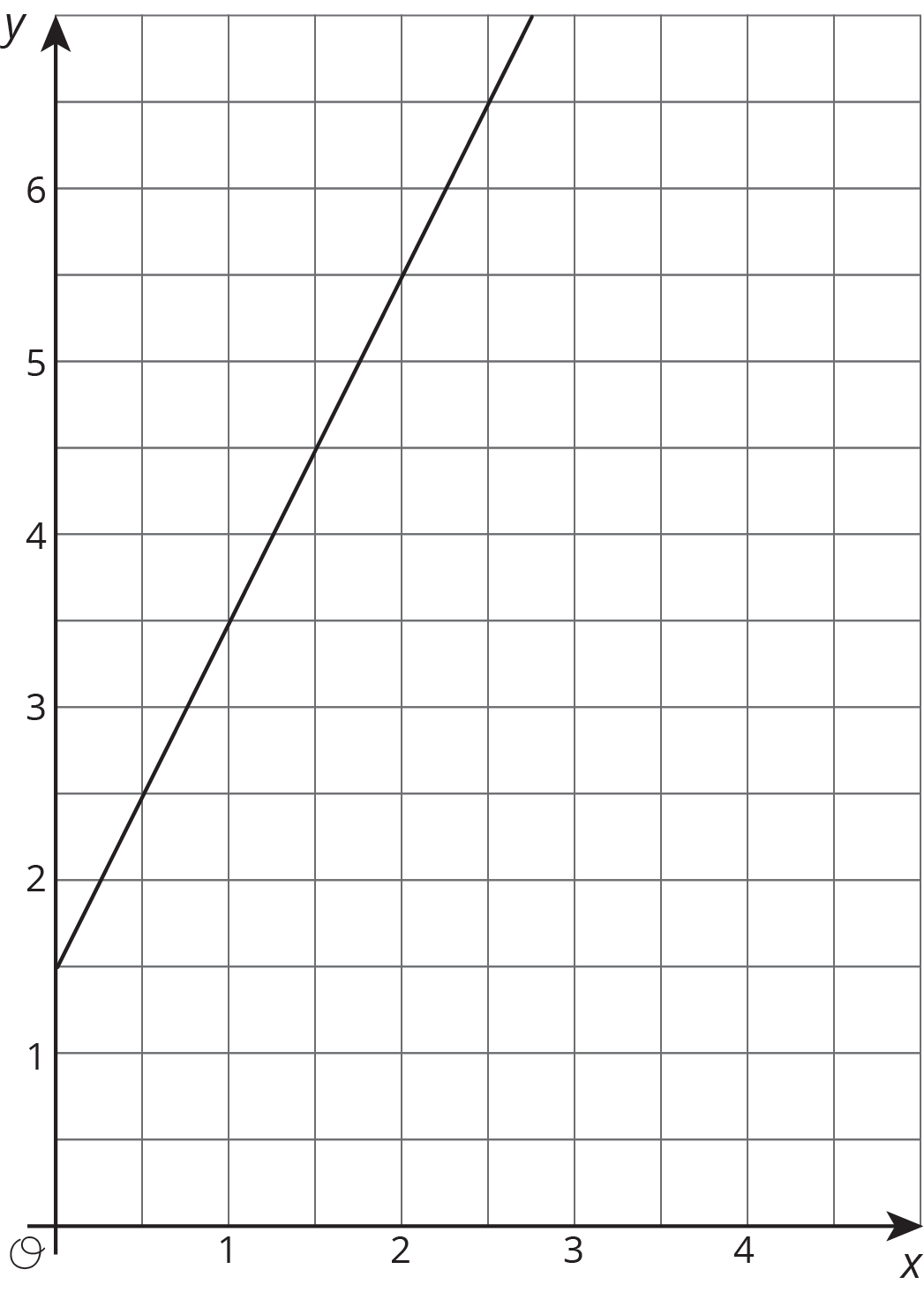
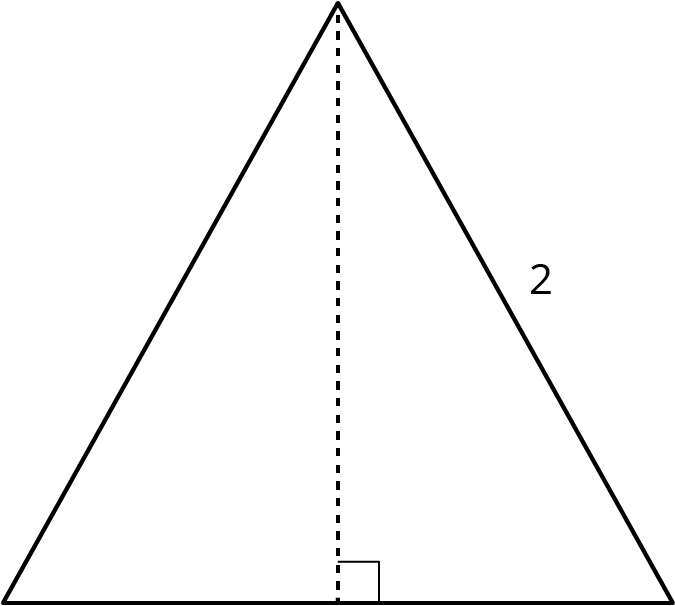
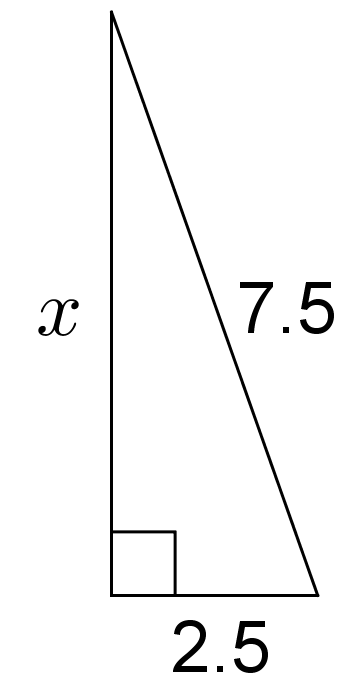
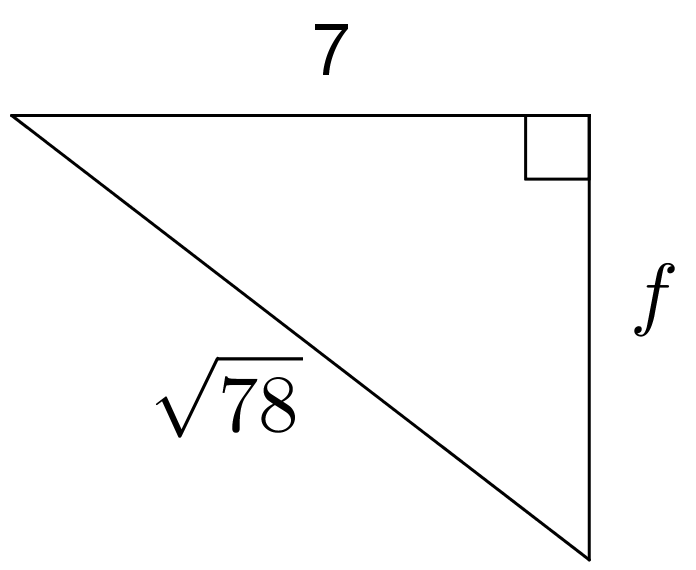
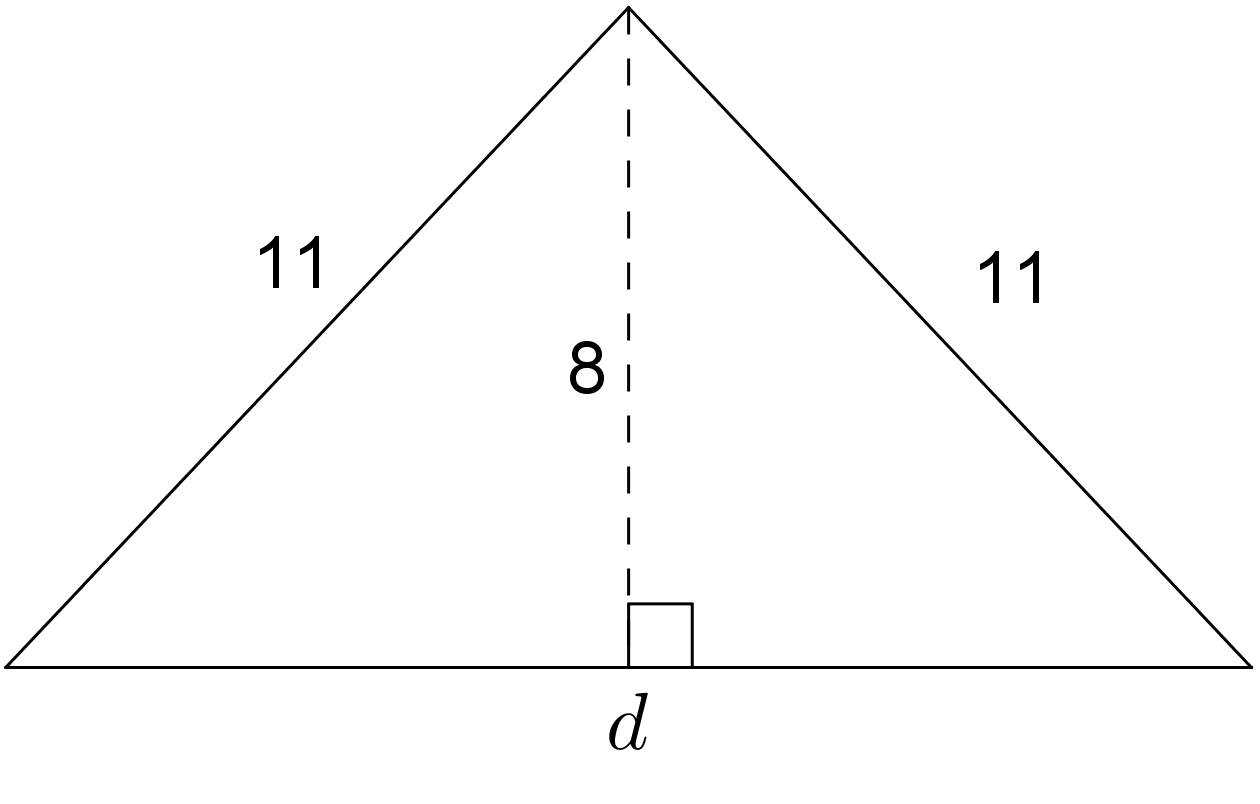
Here is a table showing the areas of the seven largest countries.
- How many more people live in Russia than in Canada?
- The Asian countries on this list are Russia, China, and India. The American countries are Canada, the United States, and Brazil. Which has the greater total area: the three Asian countries, or the three American countries?